|
Uitleg over het oplossen van $x^{2}-x-1=0$ voor de 'wiskunde en konijnen'.
Je kunt met je GR ook vergelijkingen oplossen. Meestal geeft je GR een benadering en niet een exacte oplossing.
Ga naar de Equation.
|
 |
|
Je kunt hier kiezen uit 3 mogelijkheden. We gaan eerst kijken naar F3:Solver. |
 |
|
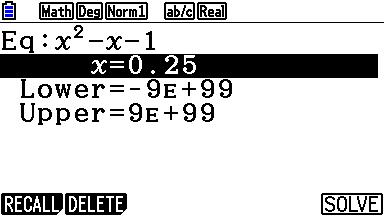
Tik op de Eq:-regel de vergelijking in die je op wilt lossen. In dit geval is dat de vergelijking $x^{2}-x-1=0$. |
 |
|
Kies voor de ondergrens Lower=0 en voor de bovengrens Upper=10. Je GR gaat dan op zoek naar een oplossing tussen 0 en 10. |
 |
|
Als je dan SOLVE klikt dan zie je op de tweede regel je oplossing staan. Dat is hier $x\approx1.619033..$. |
 |
|
Als je naar het Equation-menu gaat dan kan je ook kiezen voor F2:Polynomial. Dat zijn veeltermfuncties. Je kunt dan kiezen tussen tweedegraads-, derde graads-, en zo...
Kies voor Degree?=2.
|
 |
|
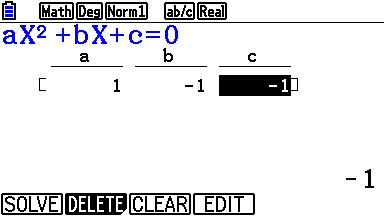
Vul de getallen voor a, b en c in en klik SOLVE. |
 |
|
Je GR geeft twee oplossingen en als je met de 'cursor' op zo'n oplossing gaat staan geeft je GR (in dit geval) zelfs de exacte oplossing...
Dat komt me bekend voor... dat lijkt wel...
|
 |