|
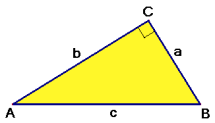
De sinus, cosinus en tangens
-
$\eqalign{\sin(\angle A)=\frac{a}{c}}$
-
$\eqalign{\cos(\angle A)=\frac{b}{c}}$
-
$\eqalign{\tan(\angle A)=\frac{a}{b}}$
|
Voorbeeld
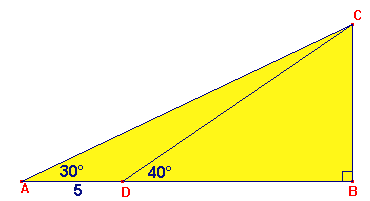
In $\Delta ABC$ geldt:
-
$\angle A=30^o$ en $\angle BDC=40^o$
-
$AD=5$
Bereken $BC$ op 1 decimaal nauwkeurig.
|
|
Tips en afspraken
Afspraak: benader (tenzij anders gevraagd) hoeken in één decimaal nauwkeurig.
Tip: Reken door met tusssenresultaten zonder af te ronden. Gebruik Ans of de geheugenplaatsen van de GR.
|
Vergelijkingen bij goniometrische berekeningen
$
\eqalign{
& x \cdot \tan (74^\circ ) = (x + 10)\tan (52^\circ ) \cr
& x \cdot \tan (74^\circ ) = x \cdot \tan (52^\circ ) + 10 \cdot \tan (52^\circ ) \cr
& x \cdot \tan (74^\circ ) - x \cdot \tan (52^\circ ) = 10 \cdot \tan (52^\circ ) \cr
& x \cdot \left( {\tan (74^\circ ) - \tan (52^\circ )} \right) = 10 \cdot \tan (52^\circ ) \cr
& x = \frac{{10 \cdot \tan (52^\circ )}}
{{\tan (74^\circ ) - \tan (52^\circ )}} \approx 5,80 \cr}
$ |