|
De standaardafwijking
Om een goed indruk te krijgen van een serie waarnemingsgetallen zou je, naast het gemiddelde, ook een maat voor spreiding moet hebben, een spreidingsmaat.
De spreidingsmaat die het meest gebruikt wordt is de standaarddeviatie of in goed Nederlands standaardafwijking.
Berekenen
Om de standaarddeviatie (van een populatie) te berekenen neem je de volgende stappen:
-
Bereken het gemiddelde
-
Neem van elk getal de afstand tot het gemiddelde
-
Neem het kwadraat van die afstanden
-
Bereken het gemiddelde van die kwadraten
-
Neem de wortel van de uitkomst
Hoe groter de standaarddeviatie hoe groter de verschillen tussen de verschillende waarnemingen.
Met de grafische rekenmachine
|
De standaardafwijking van een toevalsvariabele
Van een toevalsvariabele $X$ is $E(X)$ de verwachtingswaarde. $E(X)$ is wat je gemiddeld kunt verwachten, dus $E(X)=\overline x$
Hieronder zie je kanshistogrammen van de toevalsvariabelen $X$ en $Y$.
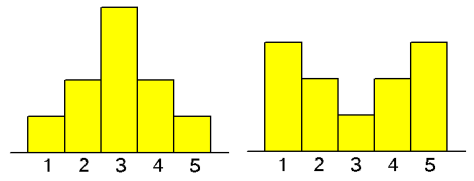
Ondanks $E(X)=E(Y)=3$ is er duidelijk een verschil tussen de kanshistogrammen. De uitkomsten van $Y$ vertonen meer spreiding van die van $X$.
De spreiding kan je uitdrukken in de standaardafwijking $\sigma_X$ en $\sigma_Y$. De berekening van gaat op dezelfde manier als bij een frequentieverdeling. In plaats van de frequenties gebruik je de kansen.
|
|
De somregels voor verwachtinswaarde en standaarddeviatie
Voor de (onafhankelijke) toevalsvariabelen $X$ en $Y$ geldt:
$E(X+Y)=E(X)+E(Y)$
$\sigma_{X+Y}=\sqrt{\sigma_X^2+\sigma_Y^2}$
|
De variantie
Het kwadraat van de standaarddeviatie wordt variantie genoemd. De somregel van de standaarddeviaties wordt dan:
$VAR(X+Y)=VAR(X)+VAR(Y)$
|