|
Groeifactoren
Bij exponentiële groei hoort de formule:
$N=b\cdot g^t$
Hierin is $b$ de beginhoeveelheid (bij $t=0$) en $g$ is de groeifactor per tijdseenheid.
Groeipercentages omzetten naar een andere tijdseenheid
Als $g$ de groeifactor is per tijdseenheid dan is de groeifactor per $n$ tijdseenheden gelijk aan $g^{n}$. Dat geldt ook voor niet-gehele $n$.
Als de groeifactor per uur bijvoorbeeld $1,25$ is dan is de groeifactor:
-
per 3 uur: $1,25^{3}$
-
per dag: $1,25^{24}$
-
per half uur: $1,25^{\frac{1}{2}}$
-
per minuut: $1,25^{\frac{1}{60}}$
Het omrekenen van een groeipercentage naar een andere tijdseenheid doe je met groeifactoren.
Een hoeveelheid neemt toe met 2,5% per uur. Met hoeveel procent neemt de hoeveelheid toe per dag?
De groeifactor per dag: $1,025^{24}\approx 1,809$
De hoeveelheid neemt toe met $80,9$% per dag.
Een formule opstellen bij exponentiële groei
Als je bij exponentiële groei op twee tijdstippen de hoeveelheid kent dan kan je een formule opstellen.
Voorbeeld
Is N=82 voor t=5 en N=246 voor t=12 dan:
-
groeifactor per 7 uur: $\frac{246}{82}$=3
-
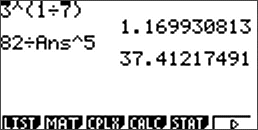
groeifactor per uur: $3^{\frac{1}{7}}\approx 1,170$
-
Formule: $N=b\cdot 1,170^{t}$
Vul in: $t=5$ en $N=82$
$b\cdot 1,170^{5}=82$
Oplossen geeft $b=37$
-
$N=37\cdot 1,170^{t}$
Denk aan de haakjes bij de rekenmachine...
|
Rekenregels voor logaritmen
L0
${}^a\log (b) + {}^a\log (c) = {}^a\log (b \cdot c)$
L1
$\begin{array}{l}
{}^a\log (b) = c \Rightarrow a^c = b \\
(a > 0 \wedge a \ne 1 \wedge b > 0) \\
\end{array}$
L2
$\begin{array}{l}
{}^a\log \left( b \right) = \frac{{\log \left( b \right)}}{{\log \left( a \right)}} \\
(zie\,\,*) \\
\end{array}$
L3
$^a \log \left( {b^p } \right) = p \cdot {}^a\log (b)$
L4
$a^{{}^a\log (b)} = b$
*)
L2 uitgebreid
$\begin{array}{l}
{}^a\log \left( b \right) = \frac{{{}^g\log \left( b \right)}}{{{}^g\log \left( a \right)}} \\
(g > 0) \\
\end{array}$
Noot
$log(x)$ betekent $^{10}log(x)$, dus met het grondtal 10. Het knopje LOG op je rekenmachine geeft de 10-de log.
Er zit op je GR ook een functie voor andere grondtallen:

Exponentiële toename
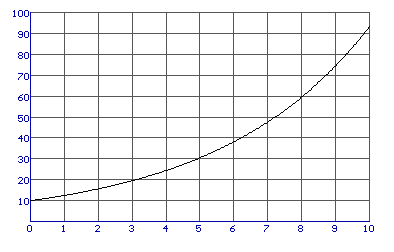
Welke formule hoort er bij deze grafiek?
|