|
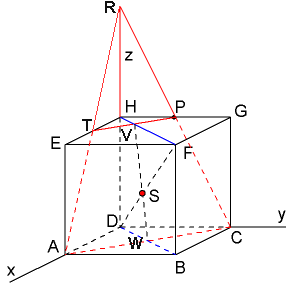
Als je het snijpunt wilt weten van $DF$ met het vlak $APC$ dan neem je voor het vlak (bijvoorbeeld) $DA$ als steunvector en vervolgens $AC$ en $AP$ als richtingsvectoren. Dat punt $R$ heb je helemaal niet nodig. Het stelsel wordt dan wel ietsje lastiger, maar uiteindelijk is dat handiger.
Een aardige oefening kan dan zijn om de coördinaten van het snijpunt $S$ van $DF$ met het vlak $APQ$ te berekenen.
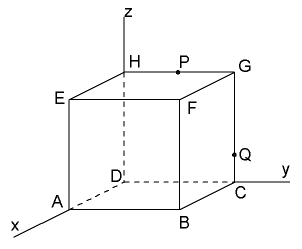
$A(4,0,0)$, $B(4,4,0)$, $F(4,4,4)$, $P(0,2,4)$ en $Q(0,4,1)$
...
Antwoord
$S\left( {1\frac{{11}}{{17}},1\frac{{11}}{{17}},1\frac{{11}}{{17}}} \right)$
Met de 'methode' uit het boek is dat een stuk lastiger.:-)
|