|
De cirkelvergelijking
De cirkel met middelpunt $M(a,b)$ en straal $r$ heeft als vergelijking:
$(x-a)^{2}+(y-b)^{2}=r^{2}$
Afleiding
Voor een punt $P(x,y)$ op afstand $r$ van $M(a,b)$ geldt:
$d(P,M)=\sqrt{(x-a)^2+(y-b)^2}=r$
Kwadrateren geeft je de cirkelvergelijking.
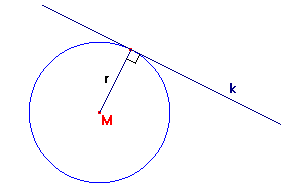
De raaklijn van een cirkel staat loodrecht op de straal naar het raakpunt.
|
De cirkelvergelijking en kwadraatafsplitsen
Je kunt de vergelijking $x^2+y^2+6x-8y+13=0$ schrijven in de vorm van de cirkelvergelijking. Dan doe je met kwadraatafsplitsen. Je kunt dan de coördinaten van het middelpunt en de straal aflezen.
$x^2+y^2+6x-8y+13=0$
$(x+3)^2-9+(y-4)^2-16+13=0$
$(x+3)^2+(y-4)^2=12$
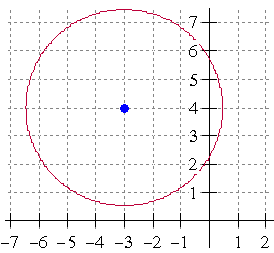
Het middelpunt is $M(-3,4)$ en $r=\sqrt{12}$
|
|
Raaklijnen in punt op cirkel
De raaklijn aan de cirkel $x^2+y^2=r^2$ in punt $A(x_A,y_A)$ heeft als vergelijking:
De raaklijn aan de cirkel $(x-a)^2+(y-b)^2=r^2$ in het punt $A(x_A,y_A)$ heeft als vergelijking:
-
$(x_A-a)(x-a)+(y_A-b)(y-b)=r^2$
De raaklijn aan de cirkel $x^2+y^2-2ax-2by+c=0$ in het punt $A(x_A,y_A)$ heeft als vergelijking:
-
$x_A x+y_A y-ax_A-ax-by_A-by+c=0$
Zie voorbeeld raaklijn in punt op cirkel
|
Raaklijnen met gegeven richtingscoëffiënt
Voor het opstellen van een vergelijking van de raaklijn $l$ met richtingscoëfficiënt $a$ aan de cirkel met middelpunt $M$ en straal $r$ zijn er drie methoden:
De discriminant-methode
Substitueer $y=ax+b$ in de cirkelvergelijking en stel $D=0$
Met de formule voor de afstand van een punt tot een lijn
Gebruik $d(M,l)=r$
Met de loodlijn door M
De lijn $k$ door $M$ en loodrecht op $l$ snijden met de cirkel geeft de raakpunten.
|
|
Raaklijnen door punt buiten de cirkel
Voor het opstellen van de vergelijkingen van de lijnen $m_1$ en $m_2$ door het punt $(p,q)$ buiten de cirkel met middelpunt $M$ en straal $r$ stel je $m:y-q=a(x-p)$ en gebruik je $d(M,m)=r$ om $a$ te berekenen.
|
Voorbeeld
Stel vergelijkingen op van de lijnen $n_1$ en $n_2$ die door het punt $B(3,2)$ gaan en raken aan de cirkel met vergelijking $(x-2)^2+(y+3)^2=13$.
|