|
De parabool als conflictlijn
Een parabool is de verzameling van alle punten met gelijke afstanden tot een punt en een lijn.
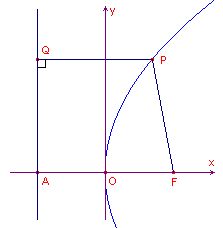
De parabool met brandpunt $F(\frac{1}{2}p,0)$ en richtlijn $l:x=\frac{1}{2}p$ heeft vergelijking $y^2=2px$
|
Top, brandpunt, richtlijn en as van parabool
Van de parabool $y^2=6x$ is de top (0,0), het brandpunt $(1\frac{1}{2},0)$, de richtlijn $x=-1\frac{1}{2}$ en de symmetrieas $y=0$.
De parabool $y^2+8y=6x+2$ ontstaat via een translatie uit de parabool van $y^2=6x$.
$y^2+8y=6x+2$
$(y+4)^2-16=6x+2$
$(y+4)^2=6x+18$
$(y+4)^2=6(x+3)$
De translatie is $(-3,-4)$
De top is $(-3,-4)$, het brandpunt $(-1\frac{1}{2},-4)$, de richtlijn $x=-4\frac{1}{2}$ en de symmetrias $y=-4$.
|
|
Parabool en raaklijnen
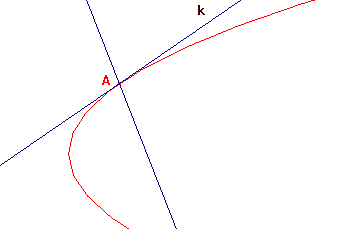
De lijn $k$ die de parabool $y^2=2px$ raakt in $A(x_A,y_A)$ heeft vergelijking:
$k:y_Ay=px+px_A$
We noemen dat 'halfsubstitutie'. De lijn door een punt van een parabool die loodrecht staat op de raaklijn in dat punt heet de normaal van de parabool in dat punt.
|
De poollijn van een punt ten opzichte van een parabool
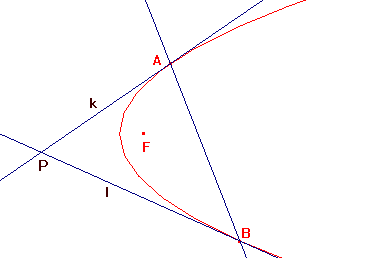
Raken de lijnen $k$ en $l$ door het punt $P(x_P,y_P)$ de parabool $y^2=2px$ in de punten $A$ en $B$, dan is:
-
de lijn $AB$ de poollijn van $P$ ten opzichte van de parabool
-
het punt $P$ de pool van de lijn $AB$ ten opzichte van de de parabool
-
$AB:y_Py=px+px_P$
|