|
Hellingsgrafiek schetsen
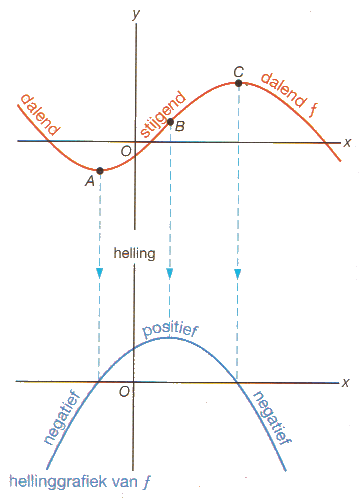
Uit de gegeven grafiek van $f$ kun je bijzonderheden van de hellingsgrafiek afleiden:
-
Bij een dalend deel van de grafiek van $f$ horen negatieve hellingen, de hellingsgrafiek ligt daar onder de $x$-as
-
In een top van de grafiek van $f$ is de helling nul. De hellingsgrafiek snijdt de $x$-as.
-
Bij een stijgend deel van de grafiek van $f$ horen positieve hellingen, dus de hellingsgrafiek ligt daar boven de $x$-as.
In een buigpunt van de grafiek van $f$ is de helling mimimaal dan wel maximaal. Een buigpunt van de grafiek van $f$ geeft derhalve een top bij de hellingsgrafiek.
|
Hellingsgrafieken plotten
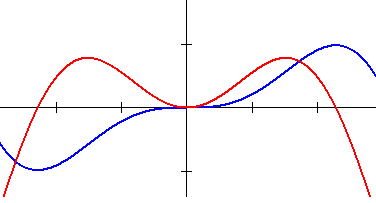
De GR heeft de mogelijkheid om hellingsgrafieken te plotten. Je maakt daarbij gebruik van:
-
$\eqalign{\frac{d}{dx}(...)|_{x=...}}$

Je kunt deze optie vinden onder OPTN en dan kiezen voor CALC.
|