|
Omgaan met formules
Bij de formule $y=5x+8$ kun je voor elke $x$ de bijbehorende $y$ berekenen. Bij $x=3$ hoort $y=5·3+8=23$ en bij $x=-4$ hoort $y=5·-4+8=-12$
Bij de formule $y=2x^2+6$ krijg je:
-
bij $x=5$ hoort:
$y=2·5^2+6=2·25+6=56$
-
bij $x=-3$ hoort:
$y=2·(-3)^2+6=2·9+6=24$
Denk aan de haakjes!
Grafieken
Behalve lineaire of kwadratische formules zijn er nog meer soorten formules, zoals:
-
wortelformules
$y=4\sqrt{x}$ of $y=2+\sqrt{x}$
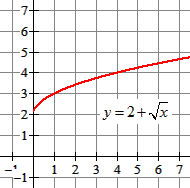
-
exponentiële formules
$y=2·1,5^x$ of $y=500·0,9^x$
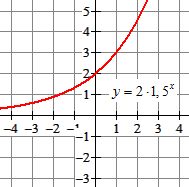

|
Lineaire en kwadratische formules
De formule $y=0,5x+3$ is een voorbeeld van een lineair verband. De grafiek is een lijn. De grafiek gaat door de $y$-as in het punt $(0,3)$ en de richtingscoëfficiënt is $0,5$, dus 1 naar rechts een half omhoog... oftewel.. twee naar rechts één omhoog...
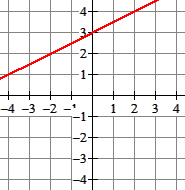
Om te controleren of een punt op de lijn ligt kun je de coördinaten van een punt invullen. Voor P(20,13) krijgt je:
$13=0,5·20+3$
$13=10+3$
$13=13$
Klopt! Dus P(20,13) ligt op de lijn.
Kwadratisch
De formule $y=0,5x^2-2x-1$ is een voorbeeld van een kwadratische formule. De grafiek is een parabool.
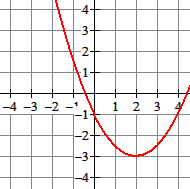
Het laagst punt van de grafiek is de top(2,-3).
Om te controleren of het punt $Q(10,31)$ op de grafiek ligt vul je $x=10$ in de formule in:
$y=0,5·10^2-2·10-1$
$y=0,5·100-20-1$
$y=50-20-1$
$y=29$
Het punt $Q(10,31)$ ligt niet op de grafiek.
|