|
Bijzonder situatie bij kwadratische ongelijkheden
Van de vergelijking $ax^2+bx+c=0$ is de discriminant gelijk aan:
$D=b^2-4ac$
Hieronder zie je enkele bijzondere situaties die kunnen optreden bij kwadratsche ongelijkheden.
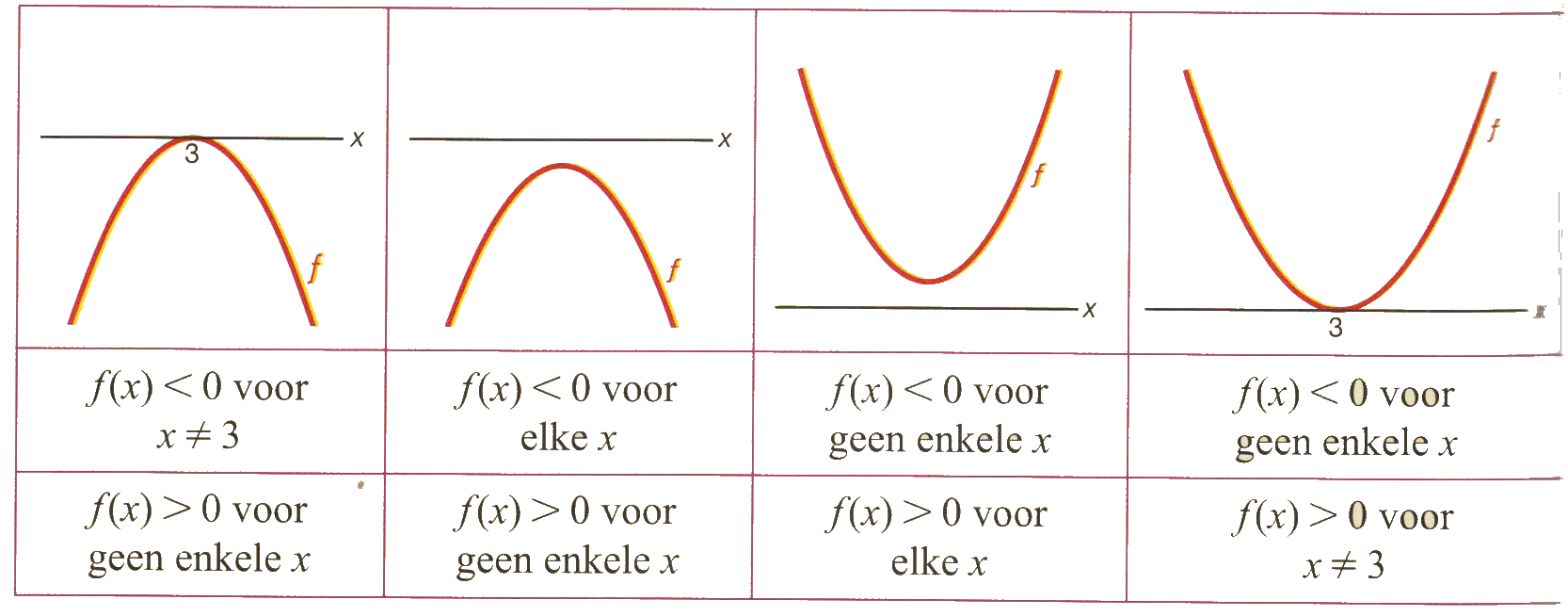
|
Ongelijkheden
Ongelijkheden van de vorm $x^2\lt c$ en $x^2\gt c$ kun je 'direct' oplossen. Een ongelijkheid als $x^2\gt10$ heeft als oplossing $x\lt-\sqrt{10}\vee x>\sqrt{10}$.
Denk aan de grafiek en je schrijft het antwoord zo op.
Voorbeeld
Los op:
-
$x^2\gt3$
-
$3x^2\lt6$
-
$2x^2-8\gt0$
Opgeloste ongelijkheden
a.
$x^2\gt3$
$x\lt-\sqrt{3}\vee x\gt\sqrt{3}$
b.
$3x^2\lt6$
$x^2\lt2$
$-\sqrt{2}\lt x\lt \sqrt{2}$
c.
$2x^2-8\gt0$
$2x^2\gt8$
$x^2\gt4$
$x\lt-2\vee x\gt2$
|