|
Frequentietabel en gemiddelde
In een frequentietabel kun je de frequenties vinden van de waarnemenigsgetallen. Dat kunnen de absolute frequenties zijn maar ook de relatieve frequenties.
$\eqalign{relatieve\,frequentie=\frac{frequentie}{totale\,frequentie}\times100\%}$
Voorbeeld
Je ziet hier een overzicht van de cijfers voor wiskunde van de 24 leerlingen uit een derde klas.
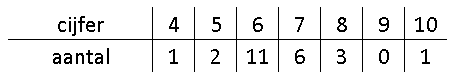
Het gemiddelde kan je berekenen met:
$
\eqalign{\frac{{4 + 2 \cdot 5 + 11 \cdot 6 + 6 \cdot 7 + 3 \cdot 8 + 10}}
{{24}} = 6,5}
$
|
Centrummaten
Naast het gemiddelde worden de centrummaten mediaan en modus veel gebruikt.
Het gemiddelde bereken je met:
$\eqalign{\frac{som\,van\,de\,waarnemingsgetallen}{totale\,frequentie}}$
Zet de getallen op volgorde van klein naar groote. De mediaan is dan het middelste getal van een oneven aantal getallen. Bij een even aantal getallen is de mediaan het gemiddelde van de middelste twee getallen.
De modus is het waarnemingsgetal met de grootste frequentie.
|
|
Klassenindeling
Om een beetje handig met grote aantallen gegevens om te kunnen gaan brengen we ze meestal onder in klassen. Zo'n klassenindeling varieert meestal van 5 tot 10 klassen met gelijke klassenbreedte.
Een klasse heeft een linker- en een rechter klassegrens. Bij het berekenen van het gemiddelde e.d. gebruik je de klassenmiddens.
Bij een klassenverdeling wordt de notatie $30-\lt40$ gebruikt. Dat zijn dan de getallen van 30 tot 40, dus 40 doet (net) niet mee in deze groep.

|
Voorbeeld
Gegeven de volgende klassenindeling:

-
bereken de 3 centrummaten
Zie centrummaten uitgewerkt
|