|
Voorbeeld
Gegeven: $f(x)=-\frac{1}{2}x^2+3x-1$.
Gevraagd: teken de grafiek van $f$.
Uitwerking
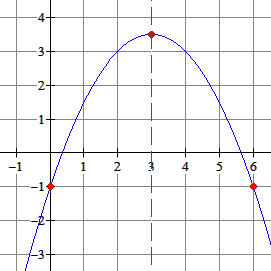 Het snijpunt met de $y$-as is het punt $(0,-1)$. Bereken het punt op gelijke hoogte: Het snijpunt met de $y$-as is het punt $(0,-1)$. Bereken het punt op gelijke hoogte:
$
\eqalign{
& - {1 \over 2}x^2 + 3x - 1 = - 1 \cr
& - {1 \over 2}x^2 + 3x = 0 \cr
& x^2 - 6x = 0 \cr
& x(x - 6) = 0 \cr
& x = 0 \vee x = 6 \cr}
$
Dat is $(0,-1)$ (hadden we al!) en het punt $(6,-1)$. De top ligt op $x=3$. Je krijgt:
$f(3)=-\frac{1}{2}\cdot3^{2}+3\cdot3-1=3\frac{1}{2}$
De top heeft als co÷rdinaten $(3,3\frac{1}{2})$
|