Uitwerkingen

Opgave 1 Van een rechthoekig terrein is de lengte 5 meter meer dan de breedte. De oppervlakte is 150 m2. Bereken de afmetingen van het terrein.	Oplossing Als je de breedte x noemt dan is de lengte x+5. Er geldt: x(x+5)=150. Deze vergelijking kan je dan oplossen.
Opgave 2 Van een rechthoekig terrein is de omtrek gelijk aan 120 m. De lengte is twee keer zo groot als de breedte. Bereken de afmetingen van het terrein.	Oplossing Noem de breedte x, dan is de lengte gelijk aan 2x. De omtrek is dan 6x. Met 6x=120 vind je dan x=20. De breedte is 20 m en de lengte is 40 m.
Opgave 3 Neem 's aan dat je 200 m prikkeldraad hebt. Wat is de oppervlakte van het grootst mogelijke terrein dat je daarmee kan afzetten!?	Oplossing Strikvraag!:-)
Opgave 4 Hieronder zie je het trapezium ABCD met twee rechte hoeken. Geef een formule voor de oppervlakte van ABCD. Wat is x als de oppervlakte gelijk is aan 30.	Oplossing Teken eerst een hulplijn. De lengte van het stuk met het vraagteken is gelijk aan x-5. De oppervlakte wordt: $ Opp = 25 + \frac{1} {2} \cdot 5 \cdot \left( {x - 5} \right) = 2\frac{1} {2}x + 12\frac{1} {2} $ Als de oppervlakte 30 is dan geldt: $ \eqalign{ & 2\frac{1} {2}x + 12\frac{1} {2} = 30 \cr & 5x + 25 = 60 \cr & 5x = 35 \cr & x = 7 \cr} $

Opgave 5 Hieronder zie je het trapezium ABCD nog een keer. Geef een formule voor de omtrek van ABCD. Wat is x als de omtrek gelijk is aan 20?

Oplossing Voor de omtrek zou je schuine zijde van driehoek PCD moeten uitdrukken in x. $ CD = \sqrt {5^2 + \left( {x - 5} \right)^2 } = \sqrt {x^2 - 10x + 50} $ De omtrek is dan gelijk aan: $ Omtrek = x + 10 + \sqrt {x^2 - 10x + 50} $ Als de omtrek 20 is dan is x=5. Een vergelijking oplossen was niet nodig, maar 't kan wel: $ \eqalign{ & x + 10 + \sqrt {x^2 - 10x + 50} = 20 \cr & x + \sqrt {x^2 - 10x + 50} = 10 \cr & \sqrt {x^2 - 10x + 50} = 10 - x \cr & x^2 - 10x + 50 = (10 - x)^2 \cr & x^2 - 10x + 50 = 100 - 20x + x^2 \cr & - 10x + 50 = 100 - 20x \cr & 10x = 50 \cr & x = 5 \cr} $

Opgave 6 Drie zijden van een gelijkbenig trapezium zijn 10 cm lang. Geef een formule voor de oppervlakte van het trapezium, uitgedruk in x.

Oplossing De oppervlakte van het trapezium is gelijk aan: $ \eqalign{ & Opp. = \frac{{z_1 + z_2 }} {2} \cdot h \cr & z_1 = 10 \cr & z_2 = 10 + 2x \cr & h = \sqrt {10^2 - x^2 } \cr & Opp. = \frac{{10 + 10 + 2x}} {2} \cdot \sqrt {10^2 - x^2 } \cr & Opp. = \left( {10 + x} \right) \cdot \sqrt {10^2 - x^2 } \cr} $

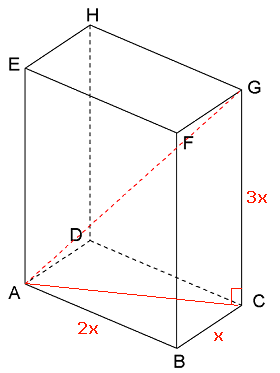
Opgave 7 In een balk ABCD.EFGH is de lengte twee keer zo groot als de breedte. De hoogte is drie keer zo groot als de breedte. Noem de breedte 'x' en druk de lengte van de lichaamsdiagonaal AG uit in x. Neem aan dat AG=$ \sqrt {42} $ Bereken de afmetingen van de balk.

Oplossing Bereken eerst AC: $ AC = \sqrt {x^2 + \left( {2x} \right)^2 } $ $ AC= \sqrt {x^2 + 4x^2 } $ $ AC = \sqrt {5x^2 } $ Bereken AG: $ AG = \sqrt {\left( {\sqrt {5x^2 } } \right)^2 + \left( {3x} \right)^2 } $ $ AG = \sqrt {5x^2 + 9x^2 } $ $ AG = \sqrt {14x^2 } $ $ \eqalign{ & \sqrt {14x^2 } = \sqrt {42} \cr & 14x^2 = 42 \cr & x^2 = 3 \cr & x = \sqrt 3 \,\,\left( {of\,\,x = - \sqrt 3 \,\,v.n.} \right) \cr} $