Voorbeeld hypergeometrische verdeling

In een vaas zitten 3 rode, 8 witte, 4 blauwe, 5 groene en 2 gele knikkers. Jan pakt steeds een knikker en legt deze NIET terug. Bereken de kans dat hij 9 keer trekken minimaal 3 groene knikkers heeft. Uitwerking De uitwerking van deze (en andere vragen) kan je vinden op kansrekening vaasmodel. Met de rekenmachine

Voor de groene knikkers: M=5 en k=2, N=22 en n=9. We willen P(X$\ge$3) berekenen. Ga naar het hoofdmenu en kies voor Statistics.
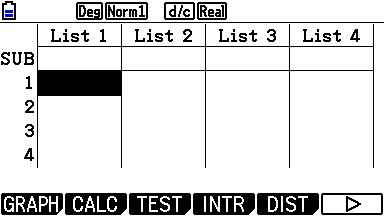
Kies voor DIST. Dat is een afkorting voor distributions. Gebruik het pijltje om verder te bladeren...
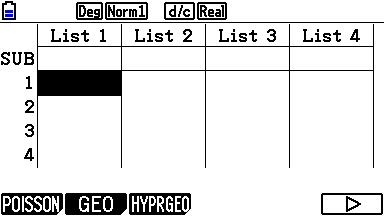
Kies voor HYPRGEO om de hypergeometrische verdeling te selecteren.
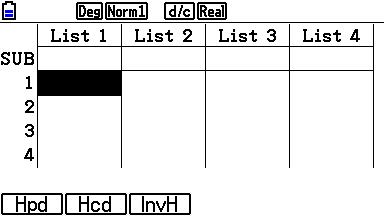
Kies vervolgens voor Hcd voor de cumulatieve hypergeometrische verdeling.
Kies voor de opties zoals je die hiernaast ziet en tik op EXE.
Je krijgt dan de kanz op 3 of meer groene kikkers... eh... knikkers...:-) P(X$\ge$3)$\approx$0,316

Je kunt hoog springen. Je kunt laag springen. Je kunt ook niet springen. Alles kan altijd beter maar dat gaat nooit vanzelf. http://www.wiswijzer.nl

©2004-2024 W.v.Ravenstein