|
Voorbeeld 1
Bij een onderzoek vindt men een 95%-betrouwbaarheidsinterval van [0,555;0,605].
-
Bereken de steekproefomvang
Uitwerking
Het interval $[0,555;0,605]$ staat voor $[\mu-2\sigma;\mu+2\sigma]$, dus tussen 0,555 en 0,605 zit $4\sigma$ verschil. Dus geldt:
-
$4\sigma=0,605-0,555=0,05$ dus $\sigma=0,0125$.
$\mu$ ligt in het midden van 0,555 en 0,605, dus geldt:
-
$\eqalign{\mu=\frac{0,555+0,605}{2}=0,58}$
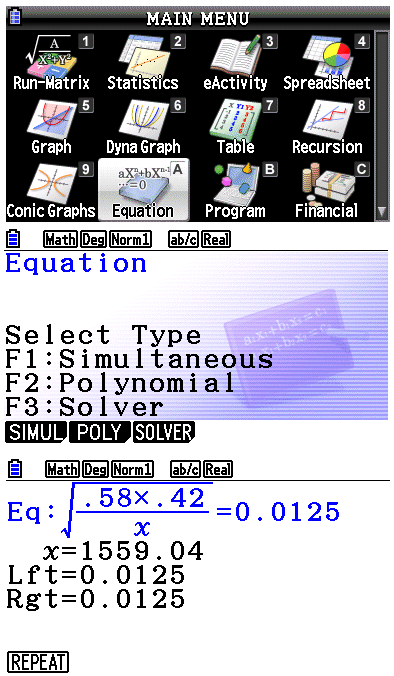
Vul nu de formule $\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$ in:
-
$\eqalign{\sigma=\sqrt{\frac{0,58\cdot0,42}{n}}=0,0125}$
Met je GR kan je dan de vergelijking oplossen.
|
 |
|
Voorbeeld 2
Bij een onderzoek onder D66-stemmers blijkt dat 55% het koningshuis wil behouden. Het bijbehorende betrouwbaarheidsinterval was [0 49;0 49;0 61]. 61].
-
Hoeveel D66-stemmers zijn ondervraagd als het een 95%-betrouwbaarheidsinterval betreft?
Uitwerking
Bij een 95%-betrouwbaarheidsinterval weet je dat $4\sigma=0,61-0,49=0,12$. Dus $\sigma=0,03$.
$\eqalign{\widehat p=\frac{0,49+0,61}{2}=0,55}$
Vul de formule $\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$ in:
$\eqalign{\sqrt{\frac{0,55\cdot0,45}{n}}=0,03}$
Deze vergelijking kan je oplossen met je GR...
Er zijn 275 D66-stemmers ondervraagd.
|

|









