|
Verticale afstanden bij grafieken
Gegeven zijn de functies $f(x)=6-\sqrt{3x+6}$ en $g(x)=-\frac{1}{2}x+5$. De lijn $x=p$ met $-2\lt p\lt10$ snijdt de grafiek van $f$ in het punt $A$ en de grafiek van $g$ in het punt $B$.
Voor de lengte $L$ van het lijstuk $AB$ geldt de formule:
$L=\sqrt{3p+6}-\frac{1}{2}p-1$
-
Bereken algebraisch de maximale waarde van $L$.
|
Minimaliseren van materiaal
Een tuinder wil voor de uitbreiding van zijn bedrijf een kas laten bouwen met een grondoppervlakte van 1800m2. Deze kas wordt rechthoekig.
De tuinder moet echter nog grond (perceel) kopen van de gemeente. Dit perceel moet zo groot zijn dat voor de kas 9 meter ruimte is en aan de achterkant en de zijde 3 meter. De tuinder wil natuurljk zo min mogelijk m2 grond kopen om zijn kosten zo laag mogelijk te houden. 1 m2 kost 95 euro.
-
Bij welke afmeting van het perceel zijn de kosten minimaal?
-
Hoeveel gaat de aankoop van grond de tuiner kosten?
-
Wat worden de afmetingen van de kas?
|
|
Uitwerking
Bepaal de afgeleide van $L$, stel de afgeleide nul en bepaal mogelijke kandidaten voor een maximum.
-
Bepaal de afgeleide:
$\eqalign{
& L = \sqrt {3p + 6} - \frac{1}{2}p - 1 \cr
& \frac{{dL}}{{dp}} = \frac{1}{{2\sqrt {3p + 6} }} \cdot 3 - \frac{1}{2} \cr
& \frac{{dL}}{{dp}} = \frac{3}{{2\sqrt {3p + 6} }} - \frac{1}{2} \cr} $
-
Stel de afgeleide nul en los op:
$\eqalign{
& \frac{3}{{2\sqrt {3p + 6} }} - \frac{1}{2} = 0 \cr
& \frac{3}{{2\sqrt {3p + 6} }} = \frac{1}{2} \cr
& 2\sqrt {3p + 6} = 6 \cr
& \sqrt {3p + 6} = 3 \cr
& 3p + 6 = 9 \cr
& 3p = 3 \cr
& p = 1 \cr} $
-
Maar een schets:
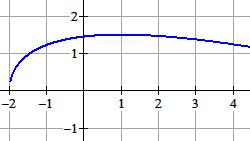
Uit de schets van $L$ volgt dat $L$ maximaal is voor $p=1$.
${L_{\max }} = \sqrt {3 \cdot 1 + 6} - \frac{1}{2} \cdot 1 - 1 = 1\frac{1}{2}$
|
Uitwerking
Maak eerst een tekening:

Vervolgens kun je de oppervlakte van het perceel uitdrukken in 'x' en op zoek gaan naar de kleinste oppervlakte.
$\eqalign{&O_{perceel}=lengte\times breedte\cr&O_{perceel}=\left({\frac{{1800}}{x} + 6} \right) \times \left({x+12}\right)\cr&O_{perceel}=1800+6x+\frac{{21600}}
{x}+72\cr&O_{perceel}=6x+\frac{{21600}}{x}+1872\cr}$
Bepaal de afgeleide:
$
\begin{array}{l}
O_{perceel} = 6x + \frac{{21600}}{x} + 1872 \\
O'_{perceel} = 6 - \frac{{21600}}{{x^2 }} \\
\end{array}
$
Neem de afgeleide nul en los op:
$
\begin{array}{l}
6 - \frac{{21600}}{{x^2 }} = 0 \\
6x^2 - 21600 = 0 \\
x^2 - 3600 = \\
x^2 = 3600 \\
x = - 60\,\,(v.n.) \vee x = 60 \\
Neem\,\,x = 60 \\
\end{array}
$
Antwoorden:
-
Bij 36 bij 72 meter zijn de kosten minimaal.
-
Het perceel kost €246.240,-
-
De kas is 30 bij 60.
|









