|
Groeifactor en groeipercentage
Van percentage naar groeifactor:
-
$\eqalign{g=1+\frac{p}{100}}$
-
Bij een toename van 32% hoort een groeifactor van 1,32
-
Bij een afname van 22% hoort een groeifactor van 0,78
Van groeifactor naar percentage:
-
$p=(g-1)·100$
-
Bij een groeifactor van 0,8 hoort een afname van 20%
-
Bij een groeifactor van 1,67 hoort een toename van 67%
Lastige gevallen:
-
Bij een toename van 450% hoort een groeifactor van 5,5
-
Bij een groeifactor van 8 hoort een toename van 700%.
|
Groeipercentages omzetten naar een andere tijdseenheid
ls $g$ de groeifactor is per tijdseenheid dan is de groeifactor per $n$ tijdseenheden gelijk aan $g^{n}$. Dat geldt ook voor niet-gehele $n$.
Als de groeifactor per uur bijvoorbeeld $1,25$ is dan is de groeifactor:
-
per 3 uur: $1,25^{3}$
-
per dag: $1,25^{24}$
-
per half uur: $1,25^{\frac{1}{2}}$
-
per minuut: $1,25^{\frac{1}{60}}$
Het omrekenen van een groeipercentage naar een andere tijdseenheid doe je met groeifactoren.
Voorbeeld
-
Een hoeveelheid neemt toe met 2,5% per uur. Met hoeveel procent neemt de hoeveelheid toe per dag?
De groeifactor per dag: $1,025^{24}\approx 1,809$, dus de hoeveelheid neemt toe met $80,9$% per dag.
|
|
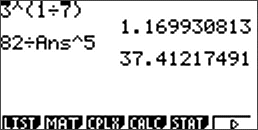
Voorbeeld 1
In 1859 werden door een Engelsman 24 wilde konijnen ingevoerd in Australie voor de plezierjacht. De natuurlijke vijand van het konijn ontbrak in Australie en er ontstond een ware konijnenplaag. In 2000 waren er ruim 300 miljoen konijnen.
-
Als we veronderstellen dat de groei exponentieel verliep, bepaal dan het groeipercentage per jaar.
Zie uitwerking voorbeeld 1
|
Voorbeeld 2
Om aan te tonen dat er sprake is van exponentiële groei moet je laten zien dat de groeifactor per tijdseenheid constant is.
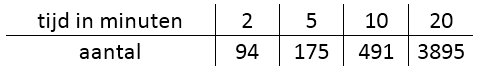
-
Laat zien dat hier sprake is van exponentiële groei.
Zie uitwerking voorbeeld 2
|