|
Archief Culinair Didactiek Documentatie Etalage Formules Fotoboeken Functies Geschiedenis ICT ICTauteur Laatste nieuws Lesmateriaal Muziek Natuur Onderwijs Ontspanning Persoonlijk Probleemaanpak Proeftuin Puzzels Rekenen Rekenmachines Ruimtemeetkunde Schoolwiskunde Snippers Systeem Taal van de wiskunde Vergelijkingen Verhalen WisFaq WisKast
|
|






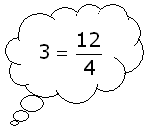 TIP
TIP