Actueel Archief Culinair Didactiek Documentatie Etalage Formules Fotoboeken Functies Geschiedenis ICT ICTauteur Laatste nieuws Lesmateriaal Muziek Natuur Onderwijs Ontspanning Persoonlijk Probleemaanpak Proeftuin Puzzels Rekenen Rekenmachines Ruimtemeetkunde Schoolwiskunde Snippers Systeem Taal van de wiskunde Vergelijkingen Verhalen WisFaq WisKast
Lineaire of eerstegraadsfunctie
Voorkennis
Lineaire formules: grafieken tekenen
Formules opstellen: formule van een lijn opstellen, evenwijdige lijnen
Lineaire vergelijkingen : vergelijkingen oplossen, snijpunten van grafieken
Lineaire functies: origineel en beeld, notatie met haakje, f(x)=ax+b
Snijpunten : snijpunten met de x- of y-s, snijpunten van grafieken
Opgave 1
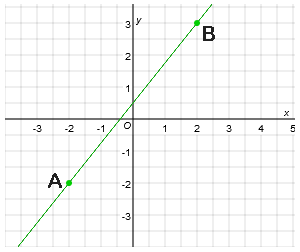
De lijn k gaat door de punten $(-2,1)$ en $(3,3)$. Geef een formule voor de lijn k.
Gegeven is de functie: $f(x) = 3x - 4$. Geef de coŲrdinaten van de snijpunten met de x- en y-as.
Gegeven zijn twee functies: $f(x) = -2x + 3$ en $g(x) = 3x - 1$. Bereken de coŲrdinaten van het snijpunt.
Formule van een lijn door twee punten
Als een lijn door $A$ en $B$ gaat dan kan je ook op deze manier een vergelijking van die lijn opstellen:
$\eqalign{a=\frac{y_B-y_A}{x_B-x_A}}$
$\eqalign{f(x)=a(x-x_A)+y_A}$
Voorbeeld
$\eqalign{a=\frac{3--2}{2--2}=\frac{5}{4}=1\frac{1}{4}}$
$\eqalign{f(x)=1\frac{1}{4}(x+2)-2}$
Toelichting
In de formule is $a$ de richtingscoŽfficient.
In de formule hebben we in het stuk na de richtingscoŽffiŽnt de coŲrdinaten van $A$ ingevuld. Dat moet niet, je had ook de coŲrdinaten van $B$ kunnen gebruiken:
Opgave 2
Laat zien dat je bij bovenstaand voorbeeld dezelfde formule krijgt als je de coŲrdinaten van $B$ invult in het tweede deel van de formule.
Opgave 3
De lijn $k$ gaat door het punt $A(5,-2)$ en heeft als richtingscoŽfficiŽnt $a=-\frac{2}{3}$.
Leg uit dat $y=-\frac{2}{3}(x-5)-2$ een vergelijking is voor $k$.
Opdracht
Ga naar https://app.dwo.nl/vo/
login als gast
oude indeling
oefenmateriaal
formules, functies en grafieken
formules voor grafieken
functies raden lineair
functie bij rechte lijnen(2)
Gebruik daarbij de methode zoals deze hierboven staat beschreven.
Laat de haakjes staan! Normaal gesproken werk je natuurlijk de haakjes weg, maar vandaag hoeft dat niet.
©2004-2026 W.v.Ravenstein






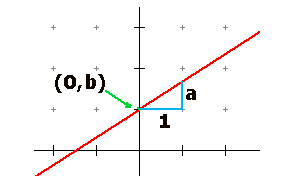 Voorkennis
Voorkennis