Stel je voor dat je deze goniometrische vergelijking wil oplossen:

$\sin(\alpha)=\frac{1}{2}$

De vraag is dan wat is de waarde van $\alpha$ zodat de $\sin(\alpha)$ gelijk aan $\frac{1}{2}$ is.

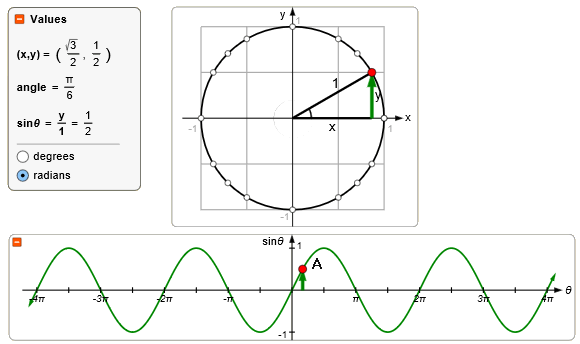
Je wist waarschijnlijk al dat de $\sin(30^o)$ gelijk is aan een $\frac{1}{2}$. In radialen is dat gelijk aan $\frac{1}{6}\pi$, dus je weet (in ieder geval) dat $\frac{1}{6}\pi$ een oplossing is.

In de grafiek is het punt $A(\frac{1}{6}\pi,\frac{1}{2})$ aangegeven...

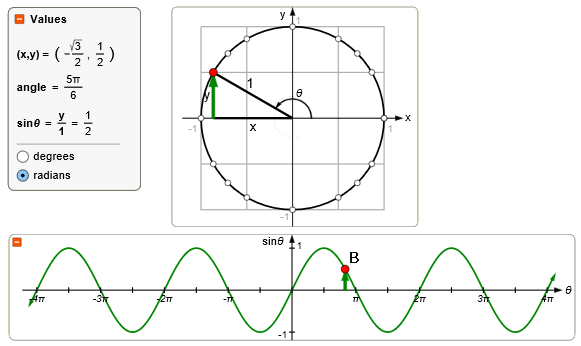
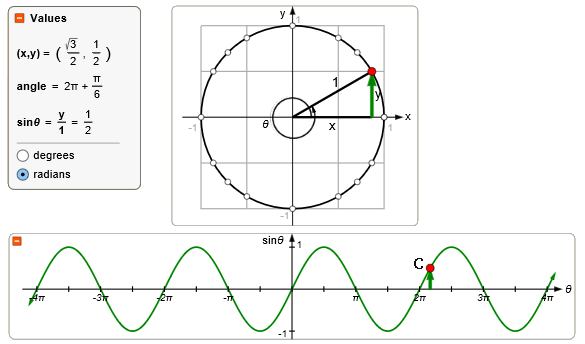
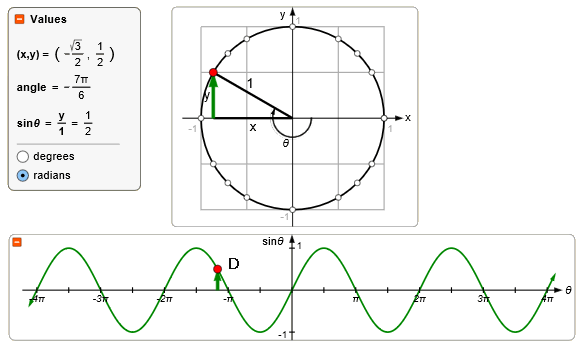
Maar er zijn nog veel meer hoeken die een sinus hebben gelijk aan een $\frac{1}{2}$. Punt B, C en zelfs D.

Kortom: er zijn oneindig veel oplossingen. Er zijn zelfs twee verschillende verzamelingen met een oneindig aantal oplossingen.

De vraag is nu: hoe kan je dat oneindig aantal oplossingen opschrijven en kan je er dan nog wel mee rekenen?

Voorbeeld

We gaan de vergelijking $2·\sin(3\alpha)+4=5$ oplossen

Stap 1

$
\eqalign{
  & 2 \cdot \sin (3\alpha ) + 4 = 5  \cr
  & 2 \cdot \sin (3\alpha ) = 1  \cr
  & \sin (3\alpha ) = \frac{1}
{2} \cr}
$

Stap 2

We weten dat $\frac{1}{6}\pi$, maar dan ook $2\frac{1}{6}\pi$ en $4\frac{1}{6}\pi$, ... maar ook $-1\frac{5}{6}\pi$ en $-3\frac{5}{6}\pi$... allemaal een sinus van een $\frac{1}{2}$ hebben.

Je kunt dit kort opschrijven als:

$\frac{1}{6}\pi+k·2\pi$ met $k\in Z$.

Maar $\frac{5}{6}\pi$ was ook goed. Op dezelfde manier schrijf je dan:

$\frac{5}{6}\pi+k·2\pi$ met $k\in Z$

Stap 3:

$
\eqalign{
  & 2 \cdot \sin (3\alpha ) + 4 = 5  \cr
  & 2 \cdot \sin (3\alpha ) = 1  \cr
  & \sin (3\alpha ) = \frac{1}
{2}  \cr
  & 3\alpha  = \frac{1}
{6}\pi  + k \cdot 2\pi  \vee 3\alpha  = \frac{5}
{6}\pi  + k \cdot 2\pi  \cr}
$

We zijn er bijna. Je moet nu nog links en rechts delen door 3. Bedenk daarbij dat je dan alle termen moet delen door 3...

Stap 4:

$
\eqalign{
  & 2 \cdot \sin (3\alpha ) + 4 = 5  \cr
  & 2 \cdot \sin (3\alpha ) = 1  \cr
  & \sin (3\alpha ) = \frac{1}
{2}  \cr
  & 3\alpha  = \frac{1}
{6}\pi  + k \cdot 2\pi  \vee 3\alpha  = \frac{5}
{6}\pi  + k \cdot 2\pi   \cr
  & \alpha  = \frac{1}
{{18}}\pi  + k \cdot \frac{2}
{3}\pi  \vee \alpha  = \frac{5}
{{18}}\pi  + k \cdot \frac{2}
{3}\pi  \cr}
$

Opgelost!

• Het oplossen van goniometrische vergelijkingen
• PHET applet bekijken