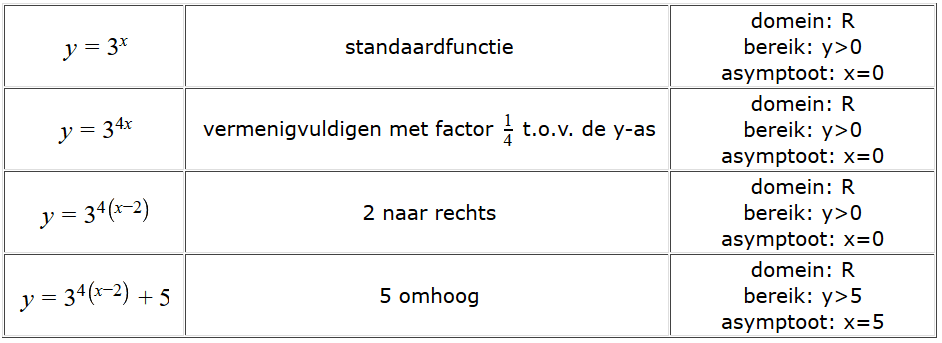
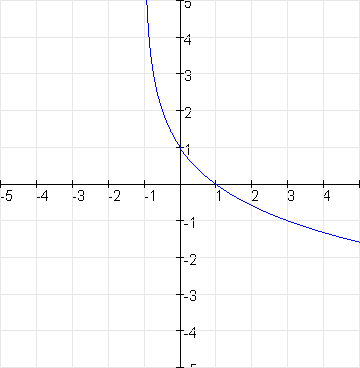
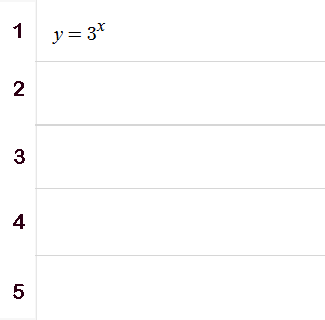Exponentiële functie

Een functie van de vorm $f(x)=b\cdot g^x$ met $g$ constant en $g\gt0$ is een exponentiële functie. We noemen $g$ de groeifactor. De variabele $x$ staat in de exponent.

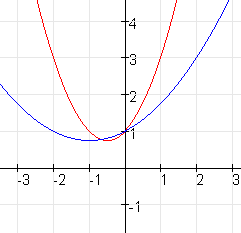
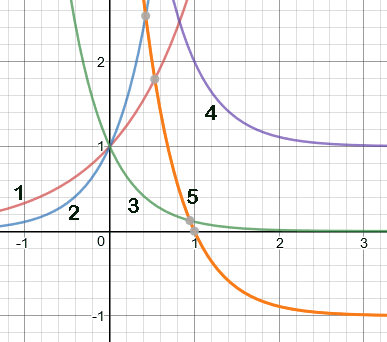
De grafiek van $f$ is stijgend als $g\gt1$ en de grafiek is dalend in het geval $0\lt g\lt1$.

De $x$-as is een asymptoot.

$D_f=R$
$B_f=<0,\to>$

De functie $f(x)=g^x$ is een standaardfunctie en de grafiek is een standaardgrafiek.

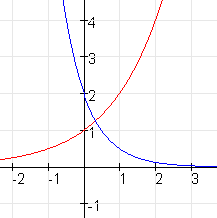
$f(x)=4\cdot2^{x-2}$
$g(x)=2\cdot\left({\frac{1}{4}}\right)^x$

Opgave 13

Geef aan met welke transformaties $f(x)=4\cdot2^{x-1}-3$ ontstaat uit de grafiek van $f(x)=2^x$.

Vermenigvuldigen t.o.v. de y-as

Vermenigvuldigen met een factor t.o.v. y-as

Vervang 'x' door '$\frac{1}{a}$x' als je wilt vermenigvuldigen met de factor 'a' t.o.v. de y-as.

Voorbeeld 1

Als je $f(x)=x^2+x+1$ bijvoorbeeld wilt vermenigvuldigen met de factor $2$ t.o.v. de $y$-as dan krijg je:

$f(x)=(\frac{1}{2}x)^2+\frac{1}{2}x+1$
$f(x)=\frac{1}{4}x^2+\frac{1}{2}x+1$

Voorbeeld 2

Geef het domein, bereik en eventuele asymptoten van:

$
g(x)=3^{4(x-2)}+5
$

Uitwerking

Opgave 14

Je ziet hier een schermafdruk uit het grafiekenprogramma. Het zijn een serie transformaties van $f(x)=3^x$. Links moeten de functievoorschriften staan van de grafieken aan de rechter kant.

Bedenk steeds welke transformatie je moet uitvoeren en geef het functievoorschrift.

Logaritmische functie

Welke transformaties heb je nodig om van de standaardfunctie $f(x)=\,^2log(x)$ te komen tot $f(x)=2-\,^2log(2x+2)$?

$f(x)=\,^2log(x)$
2 naar links
$f(x)=\,^2log(x+2)$

$f(x)=\,^2log(x+2)$
verm. met een factor $\frac{1}{2}$ t.o.v. de y-as
$f(x)=^2log(2x+2)$

$f(x)=\,^2log(2x+2)$
spiegelen in de x-as
$f(x)=-\,^2log(2x+2)$

$f(x)=-\,^2log(2x+2)$
2 omhoog
$2-\,^2log(2x+2)$

Opgave 15

Vul in:

Opgave 16

Gebruik de online rekenmachine of je grafische rekenmachine.

Teken de grafiek van $f(x)=2·\,^2log(x)$ en $g(x)=\,^2log(x^2)$. De grafieken van $f$ en $g$ lijken op elkaar maar er is een belangrijk verschil. Wat is het verschil? Leg uit.