

In een vaas zitten 8 witte, 4 blauwe en 2 rode ballen. We trekken steeds drie ballen uit de vaas zonder terugleggen.
Maak gebruik van:
| De kans P = |
aantal gunstige uitkomsten aantal mogelijke uitkomsten |
Aantal gunstige uitkomsten is 3·8·7·6=1008
Aantal mogelijke uitkomsten is 14·13·12=2184
P(2 witte ballen)=$\large\frac{1008}{2184}=\frac{6}{13}$
Er zijn eigenlijk twee soorten ballen: witte en niet-witte. Wat is nu de kans op (precies) twee witte ballen? Er zijn nu verschillende mogelijkheden: de eerste 2 ballen kunnen wit zijn en de derde niet, de eerste en de derde kunnen wit zijn, enzovoort....
Om de kans uit te rekenen kun je kijken naar één zo'n volgorde. We nemen maar wit, wit, niet-wit. We kijken naar P(w,w,n), dus de kans op precies die volgorde!
P(w,w,n) = $\large\frac{8}{14}\cdot\frac{7}{13}\cdot\frac{6}{12}=\frac{2}{13}$
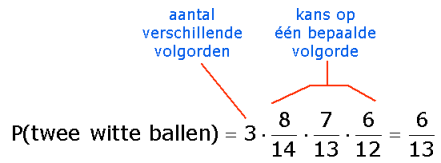
Vervolgens kijk je hoeveel verschillende volgordes je kunt maken met twee witte en een niet-witte. Dit kan op 3 verschillende manieren, dus de kans op precies twee witte ballen is 3·$\large\frac{2}{13}=\frac{6}{13}$
Je kunt dit soort vragen ook oplossen door naar combinaties te kijken. Op hoeveel manieren kan je 2 witte knikkers uit de vaas halen.
$P(2 witte)=$ $\eqalign{\frac{{8\choose2}\cdot{6\choose1}}{{14\choose3}}}$ $\approx0,462$
De eerste twee methodes zijn voor leerlingen vaak lastig. Telproblemen zijn sowieso lastig. Het vaasmodel (de hypergeometrische verdeling) kan in dit soort gevallen vaak uitkomst bieden. Op hoeveel manieren kan je 2 witte ballen kiezen uit 8 witte ballen als je niet op de volgorde let... enz. Dat gaat meestal beter.
Uiteraard blijft het zaak om te weten waar je mee bezig bent. Er bestaat niet zoiets als één manier om iets uit te rekenen. Juist niet. Maar als je begrijpt wanneer je welke rekenmethode wel of niet kan gebruiken ben je al een eind op weg.