Dat is nog niet zo eenvoudig.

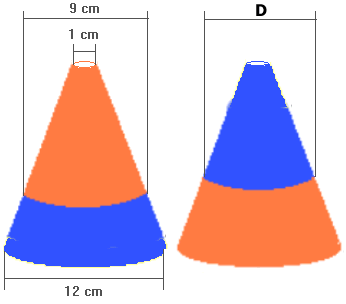
Een kegelvormige fles heeft een basisdiameter van 12cm en de kurk bovenaan heeft een diameter van 1cm. Er is nog wat vloeistof in de fles. De diameter van het bovenvlak van de vloeistof is 9cm. Veronderstel nu dat de fles wordt omgedraaid.
Dat is nog niet zo eenvoudig.
Ik heb het puntje dat links ontbreekt voor een volledige kegel de hoogte $h$ gegeven. Het plan is dan om de inhoud links uit te drukken in $h$. Vervolgens kan je dan de inhoud aan de rechter kant uitdrukken in $h$ en $D$, waarbij $D$ dan de diameter is van het ondervlak van het blauwe gedeelte.
Ik gebruik daarbij deze formule:
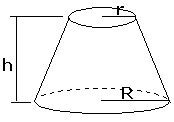
$ \eqalign{I = \frac{1} {3}\pi h\left( {R^2 + Rr + r^2 } \right)} $
Vervolgens kan je dan proberen de verschillende 'waarden' voor de variabelen te vinden.
Links
Gegeven zijn $R=6$ en $r=4,5$. De vraag is nog wat de hoogte van het blauwe gedeelte is. Je kunt laten zien dat dit $3h$ moet zijn. Ga maar na!
Je kunt de inhoud links uitdrukken in $h$:
$ \eqalign{I_{links} = \frac{1} {3}\pi \cdot 3h\left( {6^2 + 6 \cdot 4\frac{1} {2} + \left( {4\frac{1} {2}} \right)^2 } \right) = \frac{{333}} {4}\pi h} $
Rechts
Gegeven zijn $\eqalign{R=\frac{1}{2}D}$ en $\eqalign{r=\frac{1}{2}}$. Op dezelfde manier als links kun de hoogte van het blauwe deel uitdrukken in $h$. Dat wordt dan $ \left( {D - 1} \right)h $.
Invullen geeft:
$ \eqalign{I_{rechts} = \frac{1} {3}\pi \cdot \left( {D - 1} \right)h\left( {\left( {\frac{1} {2}D} \right)^2 + \frac{1} {2}D \cdot \frac{1} {2} + \left( {\frac{1} {2}} \right)^2 } \right)} $
Conclusie
Nu moet gelden:
$ I_{rechts} = I_{links} $
Als het goed is dan kan je zien dat de $h$ wegvalt. Je krijgt een vergelijking met als onbekende $D$. Oplossen geeft je dan de gevraagde diameter.
$ \eqalign{ & \frac{1} {3}\pi \cdot \left( {D - 1} \right)h\left( {\left( {\frac{1} {2}D} \right)^2 + \frac{1} {2}D \cdot \frac{1} {2} + \left( {\frac{1} {2}} \right)^2 } \right) = \frac{{333}} {4}\pi h \cr & \left( {D - 1} \right)\left( {\frac{1} {4}D^2 + \frac{1} {4}D + \frac{1} {4}} \right) = \frac{{999}} {4} \cr & \left( {D - 1} \right)\left( {D^2 + D + 1} \right) = 999 \cr & D^3 + D^2 + D - D^2 - D - 1 = 999 \cr & D^3 - 1 = 999 \cr & D^3 = 1000 \cr & D = 10 \cr} $
Het is een lastig probleem omdat je de hoogte niet kent. Uiteindelijk blijk je die ook niet nodig te hebben, maar weet dat maar 's van te voren.
Je zou in eerste instantie een concrete waarde kunnen nemen voor de hoogte van de kegel. Maar 't is praktischer om het 'afgeknotte stuk' de lengte 1 cm te geven. Met verhoudingen kom je er dan wel uit. Maar als het met een concrete waarde kan dan kan het misschien ook wel met een hoogte van $h$ voor het afgeknotte deel.