Een steeg en twee ladders
In een smalle straat zijn twee schilders bezig met het schilderen van de gevels van de tegenover elkaar staande huizen. De ene schilder heeft een ladder AC van 11 meter. De ander ladder BD is 9 m. De ladders kruisen elkaar op 4 m hoogte.- Hoe breed is de straat?
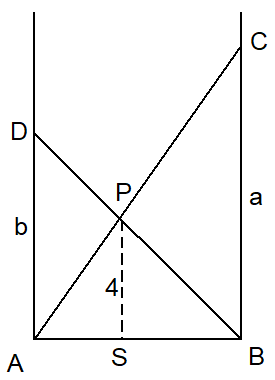 De driehoeken APS en ACB zijn gelijkvormig, evenals de driehoeken BPS en BDA. Hieruit volgt:
De driehoeken APS en ACB zijn gelijkvormig, evenals de driehoeken BPS en BDA. Hieruit volgt:
$
\eqalign{\frac{x}
{{x + y}} = \frac{4}
{a}\,\,\,{\text{en}}\,\,\,\frac{y}
{{x + y}} = \frac{4}
{b}}
$
Tellen we dit bij elkaar op, dan krijgen we:
$
\eqalign{\frac{4}
{a} + \frac{4}
{b} = 1}
$
Lossen we hieruit $a$ op, dan:
$
\eqalign{a = \frac{{4b}}
{{b - 4}}\,\,\,(1)}
$
Met behulp van de stelling van Pythagoras in de driehoeken ABC en ABD vinden we:
$
\eqalign{
& \left( {x + y} \right)^2 + a^2 = 11^2 \cr
& \underline {\left( {x + y} \right)^2 + b^2 = 9^2 } \cr
& \,\,\,\,\,\,\,\,\,\,\,\,a^2 - b^2 = 40 \cr}
$
Vul hierin (1) in:
$
\eqalign{\left( {\frac{{4b}}
{{b - 4}}} \right)^2 - b^2 = 40}
$
Oplossen geeft:
$
{\text{b}} \approx {\text{ 6}}{\text{,96}}
$