|
Stel vergelijkingen op van de lijnen $n_1$ en $n_2$ die door het punt $B(3,2)$ gaan en raken aan de cirkel met vergelijking $(x-2)^2+(y+3)^2=13$.
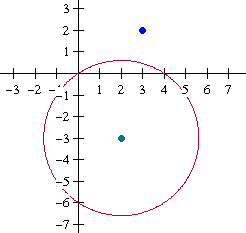
|
Stel $n:y-2=a(x-3)$ ofwel $ax-y-3a+2=0$.
De lijn $n$ raakt aan de cirkel, dus $d(M,n)=r$.
$
\eqalign{
& \frac{{\left| {a \cdot 2 - - 3 - 3a + 2} \right|}}
{{\sqrt {a^2 + ( - 1)^2 } }} = \sqrt {13} \cr
& \frac{{\left| { - a + 5} \right|}}
{{\sqrt {a^2 + 1} }} = \sqrt {13} \cr
& \left| { - a + 5} \right| = \sqrt {13a^2 + 13} \cr
& a^2 - 10a + 25 = 13a^2 + 13 \cr
& 12a^2 + 10a - 12 = 0 \cr
& 6a^2 + 5a - 6 = 0 \cr
& D = 5^2 - 4 \cdot 6 \cdot - 6 = 169 \cr
& a_{1,2} = \frac{{ - 5 \pm 13}}
{{12}} \cr
& a = - 1\frac{1}
{2} \vee a = \frac{2}
{3} \cr
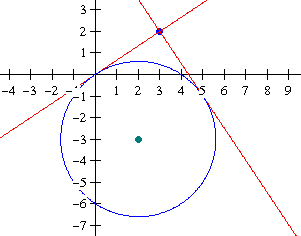
& n_1 :y = - 1\frac{1}
{2}x + 6\frac{1}
{2} \cr
& n_2 :y = \frac{2}
{3}x \cr}
$
|