|
De cosinusregel
In elke driehoek $ABC$ geldt de cosinusregel:
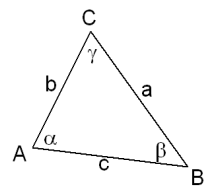
$a^2=b^2+c^2-2bc·\cos(\alpha)$
$b^2=a^2+c^2-2ac·\cos(\beta)$
$c^2=a^2+b^2=2ab·\cos(\gamma)$
Opmerking
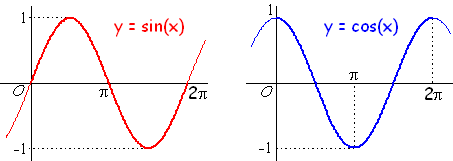
Als je te maken hebt met een stompe hoek dan is de waarde van de cosinus negatief.
|
Voorbeeld
-
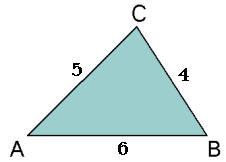
Bereken $\angle A$
(op hele graden nauwkeurig)
Uitgewerkt
$4^2=5^2+6^2-2·5·6·\cos(\alpha)$
$16=25+36-60·\cos(\alpha)$
$16=61-60·\cos(\alpha)$
$-45=-60·\cos(\alpha)$
$\eqalign{\cos(\alpha)=\frac{-45}{-60}}$
$\eqalign{\cos(\alpha)=\frac{3}{4}}$
$\alpha\approx41^\circ$
|