|
Vuistregels bij de normale verdeling
De normale verdeling is een continue kansverdeling. Kansverdelingen waarbij een continue variabele een rol speelt komen veel voor.
Als je bijvoorbeeld kijkt naar het gewicht van een pak koffie van een bepaald merk, of naar de gemiddelde opbrengst van een hectare grond of naar de lengte van een groot aantal personen dan heb je steeds te maken met een continue kansverdeling.
Bij veel discrete kansverdelingen wordt vaak gedaan alsof ze continu zijn, vooral bij grote aantallen.
Een paar eigenschappen van een normale verdeling:
-
klokvormig
-
de oppervlakte onder de kromme komt overeen met 100% van de gegevens
-
symmetrisch t.o.v. het gemiddelde.
-
gemiddelde, mediaan en modus vallen samen
-
de verdeling wordt bepaald door de verwachtingswaarde en de standaarddeviatie
-
vuistregels:
-
68% van de gegevens wijkt op z'n hoogst één keer de standaarddeviatie af van de verwachtingswaarde
-
95% van de gegevens wijkt op z'n hoogst twee keer de standaarddeviatie af van de verwachtingswaarde
Voor een normale dichtheidskromme is het mogelijk de standaarddeviatie op het oog te schatten. De afstand van het buigpunt tot het centrum (gemiddelde en mediaan) is namelijk de standaarddeviatie.
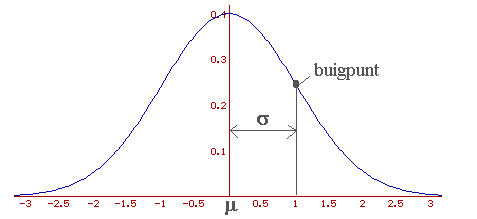 Hierboven zie je de standaardnormale verdeling. Hierbij is de verwachtingswaarde $\mu$ gelijk aan $0$ en de standaarddeviatie $\sigma$ gelijk aan 1. Met de standaardnormale verdeling en een tabel kun je allerlei uitspraken doen over alle normale verdelingen.
|
Normaal-waarschijnlijkheidspapier
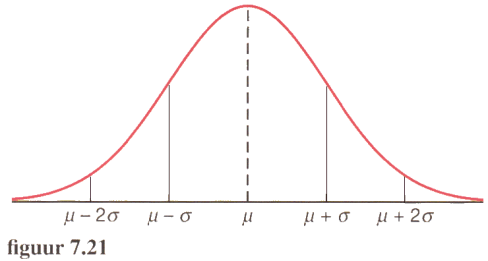
Om te onderzoeken of een steekproef uit een normaal verdeelde populatie afkomstig is kan je gebruik maken van normaal-waarschijnlijkheidspapier.
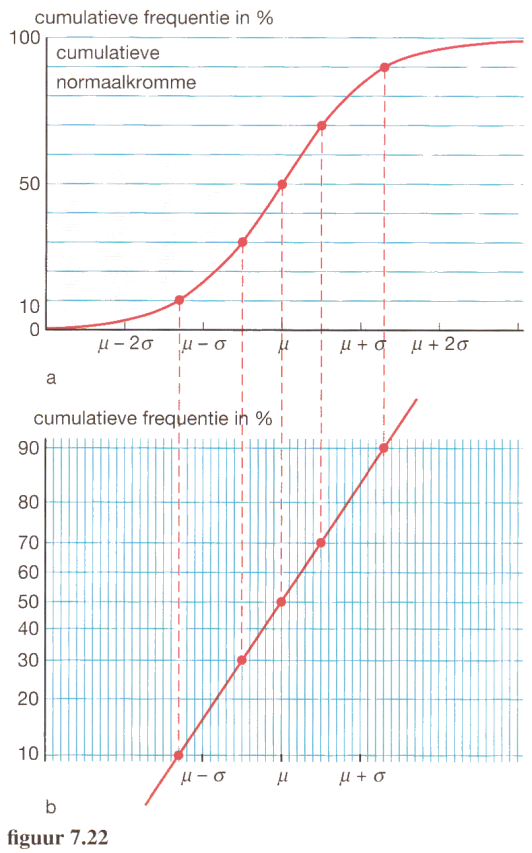
Op dit papier lees je op de verticale as de cumulatieve frequentie af. Op de horizontale as kun je zelf een geschikt schaalverderling kiezen. op de klassen uit te zetten.
Op dit papier wordt elke relatieve somfrequentiepolygoon een rechte lijn. Je kunt dat gebruiken om te testen of een verdeling bij benadering een normale verdeling voorstelt.
|
