oppervlakte basisfiguren

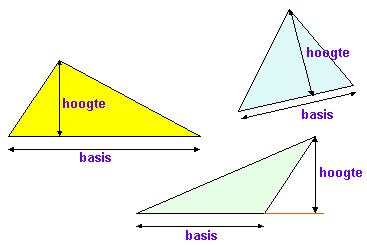
$ O_{{\text{driehoek}}}  = \frac{1} {2} \cdot b \cdot h $ Voor bijzonder driehoeken als rechthoekige, gelijkbenige of gelijkzijdige driehoeken geldt de formule natuurlijk ook, maar meestal maak je daarbij ook nog gebruik van de bijzondere eigenschappen van deze driehoeken.

$ O_{{\text{parallellogram}}}  = b \cdot h $ Voor bijzondere parallellogrammen als ruit, rechthoek en vierkant geldt deze formule natuurlijk ook, maar soms kan het dan (ook) op een andere manier.

$ O_{{\text{cirkel}}}  = \pi  \cdot r^2 $ $ O_{{\text{cirkel}}}  = \frac{1} {4} \cdot \pi  \cdot d^2 $ Waarbij $\pi\approx 3,14$

$ O_{{\text{trapezium}}}  = \frac{1} {2} \cdot \left( {a + b} \right) \cdot h $

  Oppervlakte basisfiguren