|
Het probleem van Königsberg
In het 18e eeuwse Königsberg vroegen de bewoners zich af of het mogelijk zou zijn een wandeling te maken over de vier delen van de stad die verbonden zijn door zeven bruggen en wel zo dat iedere brug precies eenmaal werd gebruik.
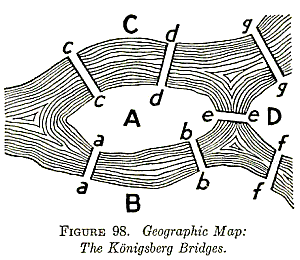
Omdat hun pogingen steeds faalden, geloofden zij, dat een dergelijke wandeling niet mogelijk was.
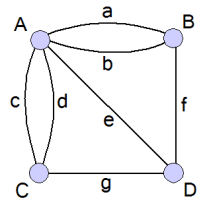
Om het probleem op te lossen kun je een graaf tekenen. Misschien dat je dan makkelijk kan zien of het mogelijk is of niet...
-
Wat denk je? Is er zo'n wandeling mogelijk?
Euler was de eerste die het probleem oploste.
"Solutio problematis ad geometriam situs pertinentis"
1736

|
Verbindingsmatrix, directe-wegenmatrix
We kijken nog een keer naar de graaf van Köningsberg.

We kunnen het al of niet verbonden zijn van de knopen in een graaf vastleggen in een matrix.
$\begin{array}{*{20}c}V&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&B&C&D\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{van}&{\begin{array}{*{20}c}A\\B\\C\\D\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}0&1&1&1\\1&0&0&1\\1&0&0&1\\1&1&1&0\\\end{array}}\right)}\\\end{array}$
Een 0 betekent dat er geen directe verbinding is en een 1 betekent dat er een directe verbinding is.
Als je ook het aantal wegen tussen de knopen wil vastleggen dan gebruik je een directe-wegenmatrix.
$\begin{array}{*{20}c}D&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&B&C&D\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{van}&{\begin{array}{*{20}c}A\\B\\C\\D\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}0&2&2&1\\2&0&0&1\\2&0&0&1\\1&1&1&0\\\end{array}}\right)}\\\end{array}$
Via matrixvermenigvuldiging kunnen we het aantal meerstapsverbindingen in een graaf berekenen. Daarmee kan je allerlei problemen oplossen.
|
|
Overgangsmatrix
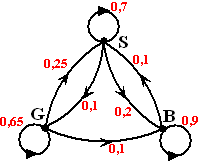
Hier zie je de graaf van een natuurgebied waarin drie soorten vegetaties (ecotypen) voorkomen, namelijk Grasland, Struikengebied en Bos. Elk jaar zal een gedeelte van die vegetaties veranderen in een andere. De getallen bij de verbindingslijnen geven de kansen daarop aan.
Stel dat er dit jaar 100 ha grasland is en 200 ha struikengebied en 300 ha bos. Hoeveel van elke soort zal er dan volgend jaar zijn?
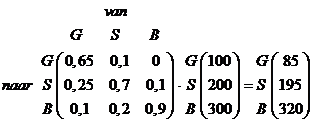
Er zal volgend jaar 85 ha grasland zijn, 195 ha struikengebied en 320 ha bos.
© h.hofstede
|
Populatievoorspellingsmatrix
Hieronder zie je een voorbeeld van een Lesliematrix. De blauwe getallen op de bovenste rij stellen de geboortecijfers voor (het gemiddeld aantal nakomelingen per individu). De rode cijfers (onder de hoofdiagonaal) stellen de overlevingskansen voor.

Bij het doorrekenen van dit soort modellen kan je voorspellingen doen over ontwikkelingen van de populatie. Neemt de populatie toe? Of neemt het juist af? Ontstaat er een evenwicht? Of zijn er periodieke verschijnselen te verwachten? Dat soort vragen...:-)

|