|
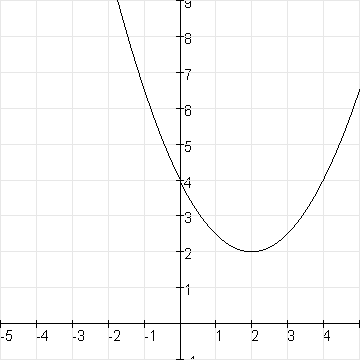
Met de topformule weer je in ieder geval dat de formule iets wordt als:
$f(x)=a(x-2)^2+2$
Nu moet $(0,4)$ er wel op liggen, dus invullen $(0,4)$ geeft:
$4=a(0-2)^2+2$
$4=4a+2$
$4a=2$
$a=\frac{1}{2}$
De formule wordt: $f(x)=\frac{1}{2}(x-2)^2+2$
|
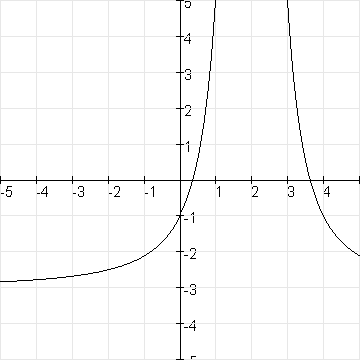
Met $x=2$ en $y=-3$ als asymptoten wordt de formule in ieder geval zoiets als:
$f(x)=\eqalign{\frac{a}{(x-2)^2}-3}$
Nu moet $(0,-1)$ er wel op liggen. Invullen van $(0,-1)$ geeft:
$\eqalign{-1=\frac{a}{(0-2)^2}-3}$
$\eqalign{2=\frac{a}{4}}$
$a=8$
De formule wordt $\eqalign{f(x)=\frac{8}{(x-2)^2}-3}$
|