|
Voorbeeld
Je kunt $f(x)=\frac{1}{2}(3x-4)^5-6$ opvatten als een transformatie van de standaardgrafiek $y=x^5$.
-
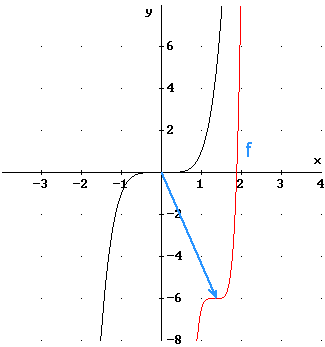
Schets de grafiek
-
Geef de coördinaten van het snijpunt van $f$ met de $y$-as
|
Uitwerking
Je kunt weten dat de grafiek door $(1\frac{1}{3},-6)$ gaat. Vanwege de vorm van de standaardgrafiek weet je hoe de grafiek van $f$ zal lopen.
Een mooi punt is het snijpunt met de $y$-as. Vul in $x=0$ en je krijgt:
$f(0)=\frac{1}{2}(3·0-4)^5-6$
$f(0)=\frac{1}{2}(-4)^5-6$
$f(0)=\frac{1}{2}·-1024-6$
$f(0)=-512-6$
$f(0)=-518$
Het snijpunt met de $y$-as is $(0,-518)$
|