|
Voorbeeld 2
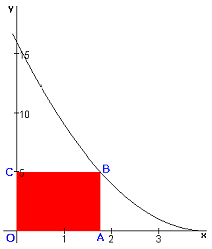
Gegeven is de functie $f(x)=(x-4)^2$. Onder de grafiek tekenen we een rechthoek $OABC$ met $O(0,0)$ en $A(p,0)$ met 0$\le$p$\le$4. $B$ ligt op de grafiek van $f$ en $C$ ligt op de $y$-as.
-
Druk de oppervlakte van $OABC$ uit in $p$.
-
Bereken m.b.v. differentiëren de maximale oppervlakte van $OABC$.
Uitwerking
De oppervlakte is gelijk aan OA·OC. Je krijgt:
De afgeleide:
$\eqalign{ & O=p(p-4)^2\cr & O=p(p^2-8p+16)\cr & O=p^3-8p^2+16p\cr & O'=3p^2-16p+16\cr}$
|
Neem O'=0 en los de vergelijking op:
$\eqalign{&3p^2-16p+16=0\cr&p=\frac{{--16\pm\sqrt{\left({-16}\right)^2-4\cdot3\cdot16}}}{{2\cdot3}}\cr&p=\frac{{16\pm\sqrt{256-192}}}{6}\cr&p=\frac{{16\pm\sqrt{64}}}{6}\cr&p=\frac{{16\pm8}}{6}\cr&p=\frac{8}{6}\vee p=4\cr&p=1\frac{1}{3}\vee p=4\cr}$
Maak een schets van de functie:
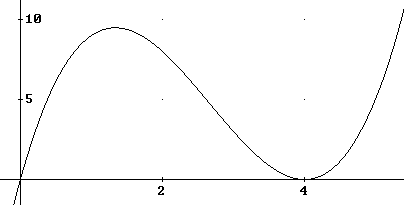
Kennelijk hebben we een maximum bij p=1$\frac{1}{3}$.
Bereken het maximum:
$\eqalign{O\left( {1\frac{1}
{3}} \right) = 9\frac{{13}}
{{27}}}$
|