|
Bernoulli-experiment
Een Bernoulli-experiment is een kansexperiment waarbij je alleen op de gebeurtenis 'succes' en 'mislukking' let.
Een binomiaal kansexperiment is een kansexperiment dat bestaat uit n gelijke Bernoulli-experimenten.
Bij een binomiaal toevalsvariabele X met parameters n en p is de kans op k keer succes gelijk aan:
P(X = k) = \left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)\cdot p^k\cdot \left( {1 - p} \right)^{n - k}
De verwachtingswaarde E(X)=n\cdot p
Voorbeeld
Je gooit met 6 dobbelstenen.
-
Wat is de kans op 2 keer zes ogen?
Antwoord
X is binomiaal verdeeld met p=\frac{1}{6} en n=6
P(X = 2) = \left( {\begin{array}{*{20}c}
6\\
2\\
\end{array}} \right) \cdot \left( {\frac{1}{6}} \right)^2\cdot \left( {\frac{5}{6}} \right)^4\approx {\rm{0}}{\rm{,201}}
|
Berekenen van binomiale kansen
Uit een vaas met 4 rode en 6 witte knikkers worden aselect, met teruglegging, drie knikkers getrokken. De stochast X is het aantal rode knikkers.
P(X=0)={3\choose0}\cdot0,4^0\cdot0,6^3=0,216
P(X=1)={3\choose1}\cdot0,4^1\cdot0,6^2=0,432
P(X=2)={3\choose2}\cdot0,4^2\cdot0,6^1=0,288
P(X=3)={3\choose3}\cdot0,4^3\cdot0,6^0=0,064
De kansverdeling staat hieronder weergegeven als staafdiagram:
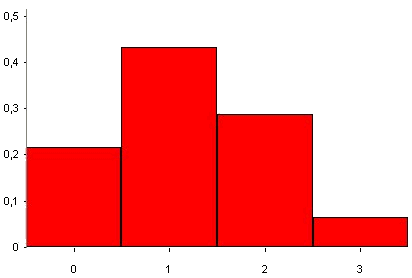
Je kunt nu ook allerlei andere kansen uitrekenen:
-
P(X\le 2)
-
P(X>1)
-
P(0\lt X\lt3)
Hier is dat een beetje flauw maar bij grotere waarden van n kunnen dat soort berekeningen als snel veel werk worden.
Met je GR kan je de kansen van de binomiale verdeling ook uitrekenen. Dat is wel zo handig...:-)
|
|
De binomiale verdeling en de GR
 Je kunt binomiale kansen uitrekenen met je GR via het run-matrix-menu en via statistics.
Via het run-matrix-menu:
Via statistics:
|
Berekenen van n
Hoe vaak moet je met een dobbelsteen gooien zodat de kans op minstens vier keer zes ogen te gooien groter is dan 0,95?
Om n te berekenen gebruik je het Table-menu van je GR:
|
|
Notaties en berekeningen
-
P(X=4)
-
P(X\le 4)
-
P(X<4)
-
P(X>4)
-
P(2< X\le 7)
-
P(2\le X <10
-
P(3\le X \le 8)
-
P(X<3\vee X>6)
Zie uitwerking
|
Multinomiale verdeling
Als een kansexperiment k verschillende uitkomsten heedt met kansen p_1, ..., p_k met p_1+...+p_k=1 op deze uitkomsten en X is het aantal keren dat de uitkomst i verkregen wordt in n onafhankelijke uitvoeringen van het experiment, dan geldt:
P(X_1 = x_1 ,...,X_k = x_k ) = \left( {\begin{array}{*{20}c}
n\\
{x_1,...,x_k }\\
\end{array}} \right)\cdot p_1^{x_1 }\cdot ...\cdot p_k^{x_k }
|
