|
Logistische groei
Bij logistische groei hoort de differentievergelijking:
$P_t=P_{t-1}+k\cdot P_{t-1}(1-$ $\Large\frac{P_{t-1}}{G}$ $)$
Hierin is $k$ de groeivoet en $G$ de grenswaarde.
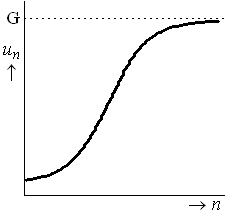
Bij logistische groei hoort een $S$-vormige kromme. De toenemende stijging gaat over in afnemende stijging op het tijdstip dat hoort bij $P=\frac{1}{2}G$
De remfactor is gelijk aan:
$1-$ $\Large\frac{P_{t-1}}{G}$
Dit is een voorbeeld van een lineaire remfactor. Exponentiële groei die geremd wordt door een lineaire remfactor heet logistiche groei.
|
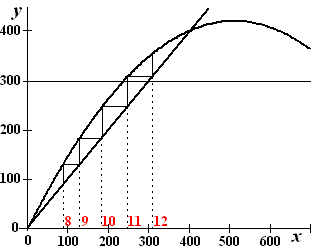
Webgrafiek van logistische groei
Je kunt elk punt van de puntenrij bij logistische groei beschrijven als:
$y=x+k\cdot x(1-\frac{x}{G})$
Dit kan je schrijven als:
$y=-\frac{k}{G}x^2+(k+1)x$.
De punten liggen op een bergparabool. Snijden met de lijn $y=x$ geeft $x=G$ als dekpunt.
©hhofstede.nl
|