|
De stelling van Thales
-
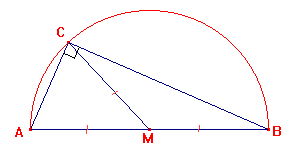
Als $C$ op een cirkel ligt met middellijn $AB$ dan is $\angle ACB$ een rechte hoek.
De omgekeerde stelling van Thales
-
Als $\angle C$ in driehoek $ABC$ recht is dan ligt $C$ op de cirkel met middellijn $AB$.

|
Koordenvierhoeken
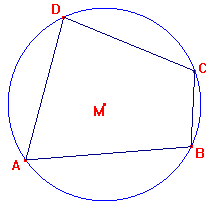
Een koordenvierhoek is een vierhoek waarbij een cirkel bestaat die door de hoekpunten gaat.
Koordenvierhoekstelling
-
De som van een paar overstaande hoeken in een koordenvierhoek is $180^o$
Omgekeerde vierhoekstelling
-
Als de som van een paar overstaande hoeken van een vierhoek gelijk is aan $180^o$ dan is de vierhoek een koordenvierhoek.
|
|
Stelling van de constante hoek
-
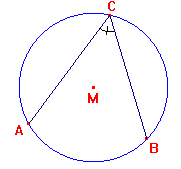
Als punt $C$ over een cirkelboog $AB$ tussen de punten $A$ en $B$ beweegt dan verandert de grootte van de omtrekshoek $ACB$ niet.
Omgekeerde stelling van de constante hoek
-
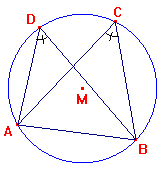
Als punt $D$ aan dezelfde kant van $AB$ ligt als punt $C$ en de hoeken $ADB$ en $ACB$ zijn even groot dan liggen $C$ en $D$ op dezelfde cirkelboog $AB$.
Gevolg
-
Als in vierhoek $ABCD$ geldt $\angle ADB=\angle ACB$ dan is $ABCD$ een koordenvierhoek.
|
De stelling van de omtrekshoek
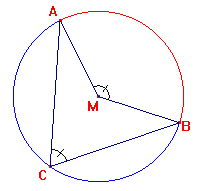
Gegeven $\angle ACB$ is een omtrekshoek op cirkelboog $AB$. Gegeven is de middelpuntshoek $AMB$.
-
Elke omtrekshoek is half zo groot als de bijbehorende middelpuntshoek.
Er geldt: $\angle ACB=\frac{1}{2}\angle AMB$

|