|
Het oplossen van de vergelijking
$ \begin{array}{l} 30000 \cdot 1,005^n - 20000 > 60000 \\ 30000 \cdot 1,005^n > 80000 \\ 1,005^n > \frac{{80000}}{{30000}} \\ \log \left( {1,005^n } \right) > \log \left( {\frac{8}{3}} \right) \\ n \cdot \log \left( {1,005} \right) > \log \left( {\frac{8}{3}} \right) \\ n > \frac{{\log \left( {\frac{8}{3}} \right)}}{{\log \left( {1,005} \right)}} \approx 196,7 \\ \end{array} $
|
 |
|
Grafisch-numerieke methoden
-
Staat er bij het oplossen van een vergelijking niet 'algebraisch' of 'exact', dan mag je (ook) gebruik maken van de grafische rekenmachine om de vergelijking op te lossen.
-
Hetzelfde geldt voor ''maxima', 'minima', 'domein', 'bereik' e.d.
-
Geef bij je oplossing de optie(s) van de GR die je gebruikt hebt.
-
Geef alle oplossingen in het gevraagd aantal decimalen en rond verstandig af.
algemene vaardigheden
|
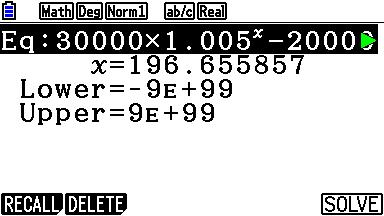
Maar je kunt ook de hele vergelijking door je GR laten oplossen. Het gaat om een benadering, dus waarom niet?
|