|
Opgave 1
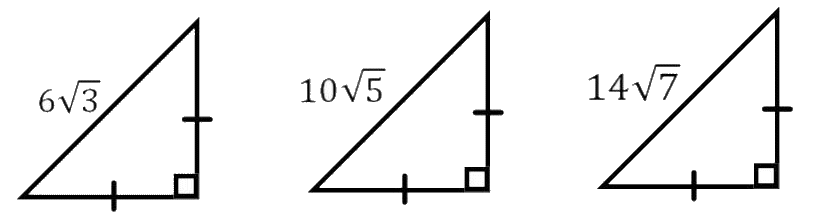
-
Bereken exact de lengte van de rechthoekszijden van bovenstaande driehoeken.
Wat valt je op?
|
Uitwerking
Je hebt hier te maken met een 45-45-90-driehoek. Je kent de verhouding van de rechthoekzijde en de schuine zijde.
$
\eqalign{
& \frac{1}
{{\sqrt 2 }} = \frac{z}
{{6\sqrt 3 }} \Rightarrow \sqrt 2 \cdot z = 6\sqrt 3 \cr
& z = \frac{{6\sqrt 3 }}
{{\sqrt 2 }} = \frac{{6\sqrt 3 }}
{{\sqrt 2 }} \cdot \frac{{\sqrt 2 }}
{{\sqrt 2 }} = \frac{{6\sqrt 6 }}
{2} = 3\sqrt 6 \cr}
$
Je krijgt: $
3\sqrt 6 ,\,\,5\sqrt {10} ,\,\,7\sqrt {14} ,\,\,...
$
|
|
Opgave 2
-
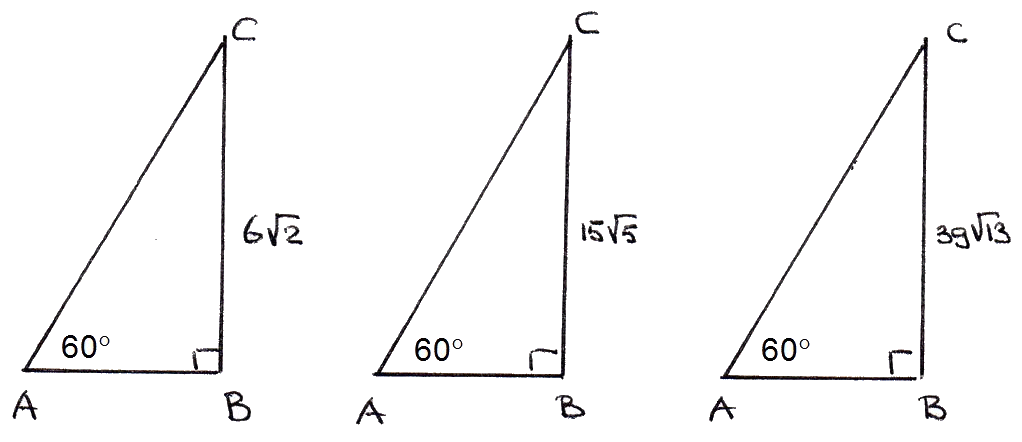
Bereken steeds exact de lengte van AB.
Wat valt je op?
|
Uitwerking
Je hebt hier te maken met een 30-60-90-driehoek. Je kent de verhouding tussen de twee rechthoekszijden.
$
\eqalign{
& \frac{{\sqrt 3 }}
{1} = \frac{{6\sqrt 2 }}
{{AB}} \Rightarrow AB \cdot \sqrt 3 = 6\sqrt 2 \cr
& AB = \frac{{6\sqrt 2 }}
{{\sqrt 3 }} = \frac{{6\sqrt 6 }}
{3} = 2\sqrt 6 \cr}
$
Je krijgt: $
2\sqrt 6 ,\,\,5\sqrt {15} ,\,\,13\sqrt {39} ,\,\,...
$
|