uitwerkingen

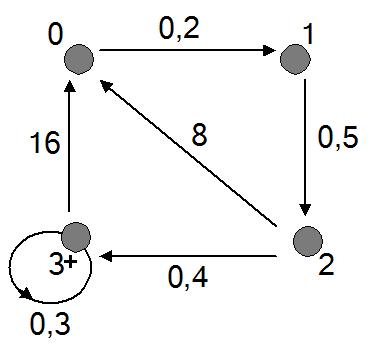
Opdracht Je ziet hier 4 generaties van een insectensoort. Er zijn 0-jarigen, 1-jarigen, 2-jarigen en insecten van 3 jaar en ouder. Geef de overgangsmatrix. Neem aan dat je met 100 0-jarige insecten begint. Geef dan de generaties van de komende 4 jaar. Neem aan dat je met 100 0-jarige, 100 1-jarige, 100 2-jarige en 100 3+-jarige begin. Hoe is de verdeling na 10 jaar? Wat is de kans van een 0-jarige de 6-jarige leeftijd bereikt?

$ \left( {\begin{array}{*{20}c}    M & {van}  \\    {naar} & {\begin{array}{*{20}c}    {} & 0 & 1 & 2 & 3  \\    0 & 0 & 0 & 8 & {16}  \\    1 & {0,2} & 0 & 0 & 0  \\    2 & 0 & {0,5} & 0 & 0  \\    3 & 0 & 0 & {0,4} & {0,3}  \\ \end{array}}  \\ \end{array}} \right) $ $ \left( {\begin{array}{*{20}c}    {100}  \\    0  \\    0  \\    0  \\ \end{array}} \right) \to \left( {\begin{array}{*{20}c}    0  \\    {20}  \\    0  \\    0  \\ \end{array}} \right) \to \left( {\begin{array}{*{20}c}    0  \\    0  \\    {10}  \\    0  \\ \end{array}} \right) \to \left( {\begin{array}{*{20}c}    80  \\    0  \\    0  \\    4  \\ \end{array}} \right) \to \left( {\begin{array}{*{20}c}    {64}  \\    16  \\    0  \\    {1,2}  \\ \end{array}} \right) $ Of... bereken $M^{4}·K$              Bereken $M^{10}·K$ $ \left( {\begin{array}{*{20}c}    0 & 0 & 8 & {16}  \\    {0,2} & 0 & 0 & 0  \\    0 & {0,5} & 0 & 0  \\    0 & 0 & {0,4} & {0,3}  \\ \end{array}} \right)^{10}  \times \left( {\begin{array}{*{20}c}    {100}  \\    {100}  \\    {100}  \\    {100}  \\ \end{array}} \right) = \left( {\begin{array}{*{20}c}    {4125}  \\    {790}  \\    {393}  \\    {144}  \\ \end{array}} \right) $ $ 0,2 \cdot 0,5 \cdot 0,4 \cdot 0,3^3  \approx 0,001 $