Los op:

• $x^3+9x=18$

Oplossing:

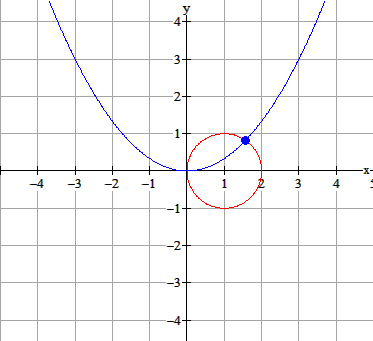
• Teken $x^2=3y$
• Teken $(x-1)^2+y^2=1$
• Bepaal de $x$-coördinaat van het snijpunt.
• $x\approx1,6$
• Opgelost...:-)

Uitwerking

• $y=\frac{1}{3}x^2$
• $(x-1)^2+y^2=1$

Geeft:

$
\eqalign{
  & (x - 1)^2  + \left( {\frac{1}
{3}x^2 } \right)^2  = 1  \cr
  & x{}^2 - 2x + 1 + \frac{1}
{9}x^4  = 1  \cr
  & x{}^2 - 2x + \frac{1}
{9}x^4  = 0  \cr
  & 9x{}^2 - 18x + x^4  = 0  \cr
  & x(x^3  + 9x - 18) = 0  \cr
  & x = 0 \vee x^3  + 9x = 18 \cr}
$

$x\approx1,6$