Kenmerken opsporen met de GR

Gegeven $f(x)=3·sin^2(x)+1$

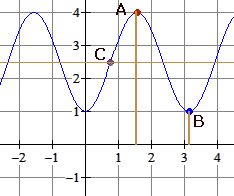
Met de GR kan je de coördinaten van de toppen $A$ en $B$ bepalen.

$A(\frac{1}{2}\pi,4)$ en $B(\pi,1)$

Je weet dan het maximum $y_A=4$ en het minimum $y_B=1$. Je weet dan de evenwichtsstand en de amplitude.

$\eqalign{a=\frac{1+4}{2}=2\frac{1}{2}}$
$\eqalign{b=\frac{4-1}{2}=1\frac{1}{2}}$

...en dan de rest

Je weet ook dat het verschil:
$\eqalign{x_B-x_A=\pi-\frac{1}{2}\pi=\frac{1}{2}\pi}$ de halve periode moet zijn. Je weet dan ook de periode.

$\eqalign{c=\frac{2\pi}{\pi}=2}$

Als je de evenwichtslijn weet kan je ook de coördinaten van $C$ bepalen. $C$ ligt $\frac{1}{4}\pi$ naar links t.o.v. $A$. Je weet dan de horizontale verschuiving.

$\eqalign{d=\frac{1}{4}\pi}$

Zodat het functievoorschrift gelijk is aan:

$y=2\frac{1}{2}+1\frac{1}{2}sin(2(x-\frac{1}{4}\pi))$