Opgave 1

Een hardloper houdt onderweg zijn tussentijden bij:

• Bereken de gemiddelde snelheid op het interval [10,21]

Opgave 2

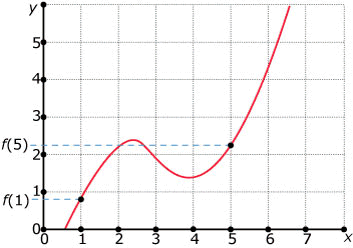
• Bereken de gemiddelde verandering op $[1,5]$

Opgave 3

Gegeven $f(x)=x^2+5x$.

• Bereken het differentiequotiënt op $[-5,1]$

Opgave 4

Gegeven is de formule $\eqalign{s=8-\frac{5}{t+2}}$. Hierin is $s$ de afgelegde weg in meter na $t$ seconden.

• Benader in m/s de snelheid op $t=1$ en op $t=2$. Neem beide keren $\Delta t=0,01$ en rond af op 2 decimalen.

Opgave 5

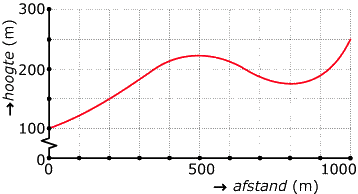
Bij het begin van een berghelling staat een waarschuwingsbord met daarop een helling van 15%. Deze grafiek geeft die berghelling weer. Horizontaal is de afstand uitgezet die je hemelsbreed hebt afgelegd en verticaal de hoogte waarop je je dan bevindt.

1. Hoeveel bedraagt de gemiddelde hoogteverandering per meter bij zo'n hellingspercentage?
2. Hoeveel bedraagt de gemiddelde hoogteverandering gerekend over de gehele berghelling?
3. Klopt het waarschuwingsbord?
4. Bereken het gemiddelde hellingspercentage op het interval ${\displaystyle [200;500]}$.
5. Schat de steilste helling van deze berghelling.

Opgave 6

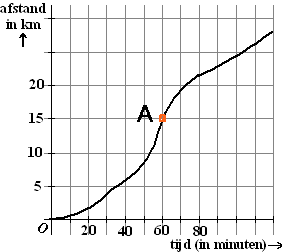
• Geef een schatting van snelheid in km/uur in het punt A.

Opgave 7

Teken een tijd-afstandgrafiek met op de horizontale as de tijd $t$ in seconden en op de verticale as de afstand $s$ in meter waarbij het volgende geldt:

• op $[0,5]$ is de gemiddelde snelheid 20 m/s
• op $t=5$ is de snelheid 20 m/s
• op $[0,8]$ is de gemiddelde snelheid 15 m/s
• op $t=8$ is de snelheid 15 m/s

Opgave 8

Je kunt $f(x)=\frac{1}{2}(3x-4)^5-6$ opvatten als een transformatie van de standaardgrafiek $y=x^5$.

• Schets de grafiek
• Geef de coördinaten van het snijpunt van $f$ met de $y$-as

Opgave 9

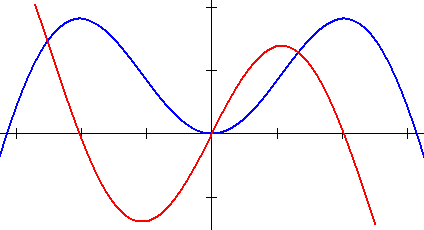
• Wat is de functie en wat is de afgeleide?

Opgave 10

Differentieer:

$
\eqalign{
& f(x) = x^2 + 4x + 3 \cr
& g(x) = 4x^9 - x \cr
& h(x) = (3x - 2)^2 \cr
& k(x) = \left( {x^2 - 1} \right)\left( {x^2 + 1} \right) \cr}
$

Opgave 11

Bepaal de afgeleide:

$
\eqalign{
& f(x) = 5x^2 + 4t \cr
& g(t) = 5x^2 + 4t \cr
& h(z) = 5x^2 + 4t \cr}
$

Opgave 12

Differentieer:

$
\eqalign{
& f(x) = ax^2 + bx + c \cr
& g(x) = (x - 1)^3 \cr
& h(x) = 2x\left( {x - 1} \right)^3 - x^2 \left( {x - 1} \right)^2 \cr}
$