|
Opgave
Bepaal de cirkelvergelijking van de cirkel met middelpunt $M(2,0)$ die raakt aan de lijn $y=x$
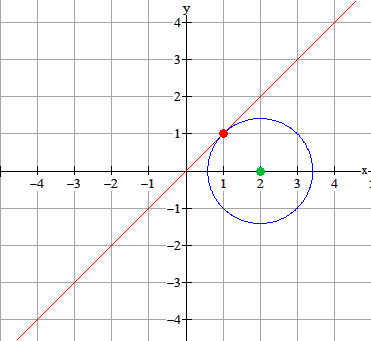
|
Uitwerking
Los het volgende stelsel op en eis dat er één oplossing is:
$
\eqalign{
& (x - 2)^2 + y^2 = r^2 \cr
& y = x \cr}
$
Invullen geeft:
$
\eqalign{
& (x - 2)^2 + x^2 = r^2 \cr
& x^2 - 4x + 4 + x^2 = r^2 \cr
& 2x^2 - 4x + 4 - r^2 = 0 \cr
& D = \left( { - 4} \right)^2 - 4 \cdot 2 \cdot \left( {4 - r^2 } \right) = 8r^2 - 16 \cr
& D = 0 \cr
& 8r^2 - 16 = 0 \cr
& r = - \sqrt 2 \,\,(v.n.) \vee r = \sqrt 2 \cr}
$
De vergelijking is:
$
(x - 2)^2 + y^2 = 2
$
|