
De wortel van...
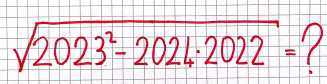
Uigewerkt
$
\eqalign{
& \sqrt {2023^2 - 2024 \cdot 2022} = \cr
& \sqrt {2023^2 - \left( {2023 + 1} \right) \cdot \left( {2023 - 1} \right)} = \cr
& \sqrt {2023^2 - \left( {2023^2 - 1^2 } \right)} = \cr
& \sqrt {2023^2 - 2023^2 + 1} = \sqrt 1 = 1 \cr}
$



©2004-2025 Wiskundeleraar - login
|