Uitgewerkt

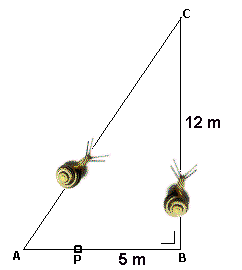Neem $AP=x$. Er geldt:

$AC^2=(x+5)^2+12^2$
$AC=\sqrt{(x+5)^2+12^2}$

Nu geldt:

$\sqrt{(x+5)^2+12^2}+x=17$

Oplossen geeft: $x=2\frac{8}{11}$

Mooiere oplossing:

Neem $AP=x$. Dan is $AC=17-x$.

Stelling van Pythagoras:

$
(x + 5)^2  + 12^2  = (17 - x)^2
$

Oplossen geeft:

$ \begin{array}{l}  (x + 5)^2  + 12^2  = (17 - x)^2  \\  x^2  + 10x + 25 + 144 = 289 - 34x + x^2  \\  44x = 120 \\  x = 2\frac{8}{{11}} \\  \end{array} $