|
Samengesteld kansexperiment
Een samengesteld kansexperiment bestaat uit twee of meer kansexperimenten. Kansexperimenten zijn onafhankelijk als ze elkaars uitkomsten op geen enkele manier beinvloeden
Voorbeeld 1
Je gooit met een munt en een dobbelsteen.
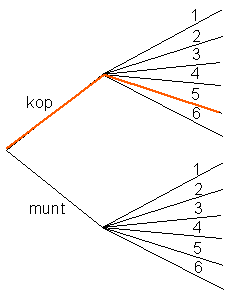
Gebeurtenis $A$: je gooit met de munt kop
Gebeurtenis $B$: je gooit 5 ogen met de dobbelsteen
De gebeurtenissen $A$ en $B$ zijn onafhankelijk.
|
Productregel
Als twee gebeurtenissen $A$ en $B$ onafhankelijk zijn dan geldt:
$P(A\cap B)=P(A)\cdot P(B)$
Samengestelde kansexperimenten kan je kansen berekenen met een boomdiagram. De kansen bij de takken die je dan tegenkomt kan je dan vermenigvuldigen.
Bij voorbeeld 1:
$A$: je gooit kop
$B$: je gooit 5 ogen
$P(A\cap B)=P(A)\cdot P(B)=\frac{1}{2}\cdot\frac{1}{6}=\frac{1}{12}$

|
|
Voorbeeld 2
Bij een wedstrijd wint diegen die twee sets wint een partij bestaat dus uit twee of drie sets. Anne en Babette spelen. Men veronderstelt dat men het volgende model volgt:
-
de kans om eerste set te winnen is 50%
-
de winnaar van set een heeft 40% kans om set twee te winnen
-
indien een derde set moet worden gespeeld heeft de winnaar van de tweede 40% kans om de derde te winnen
Kansboom
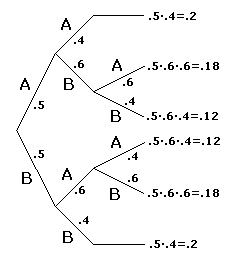
|
Regels voor berekenen van kansen
Bij het berekenen van kansen gebruik je:
-
de productregel
-
de somregel
-
de complementregel
Somregel
Als gebeurtenis $G$ en $H$ geen enkele uitkomst gemeenschappelijk hebben dan geldt:
$P(G\,\,of\,\,H) = P(G) + P(H)$
Complementregel
Als er in de omschrijving van een gebeurtenis 'minstens', 'hoogstens', 'meer dan', 'minder dan' of 'niet' voorkomt dan kan de complementregel je rekenwerk besparen.
$P(G)=1-P(niet\,\,G)$
Zie de somregel en de complementregel voor voorbeelden.
|









