|
Trekken met en zonder terugleggen
Je pakt 3 knikkers uit een vaas met 3 rode en 4 witte knikkers. Noem het aantal rode knikkers $X$.
Zonder terugleggen
$P(X=1)=
\left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right)
$ $\Large\cdot\frac{3}{7}\cdot\frac{4}{6}\cdot\frac{3}{5}$ $\approx0,514$
Met terugleggen
$P(X=1)=
\left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right)
$ $\Large\cdot\frac{3}{7}\cdot(\frac{4}{7})^2$ $\approx0,420$
|
Eén vraag, drie oplossingen...
In een vaas zitten 8 witte, 4 blauwe en 2 rode ballen. We trekken steeds drie ballen uit de vaas zonder terugleggen.
-
Bereken de kans op 2 witte ballen.
1e manier
Aantal gunstige uitkomsten is 3·8·7·6=1008
Aantal mogelijke uitkomsten is 14·13·12=2184
$P({\rm{2}}\,\,{\rm{witte}})$=$\large\frac{1008}{2184}=\frac{6}{13}$
2e manier
$P(w,w,n)$ = $\large\frac{8}{14}\cdot\frac{7}{13}\cdot\frac{6}{12}=\frac{2}{13}$
$
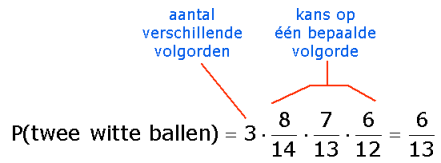
P({\rm{2}}\,\,{\rm{witte}}) = 3 \cdot \frac{8}{{14}} \cdot \frac{7}{{13}} \cdot \frac{6}{{12}} = \frac{6}{{13}}
$
3e manier
$P({\rm{2}}\,\,{\rm{witte}})=$ $\Large\frac{{8\choose2}\cdot{6\choose1}}{{14\choose3}}$ $=\frac{6}{13}$
Zie één vraag drie uitwerkingen
|
|
Formules opstellen
Wat je 'normaal gesproken' met getallen doet kan je, ook bij kansrekenen, ook met variabelen doen. Dat zijn immers ook getallen, ook al weet je niet precies wat ze (kunnen) zijn.
Je hebt een vaas met $n$ knikkers. Daarvan zijn er 4 rood en de rest is wit. Je kunt dan formules opstellen voor verschillende kansen. Neem aan dat je met terugleggen twee knikkers trekt:
$
\begin{array}{l}
P(0\,\,rood) = \large\left( {\frac{{n-4}}{n}} \right)^2=\frac{{n^2-8n+16}}{{n^2 }}\\
P(1\,\,rood) = 2 \cdot \large\frac{4}{n} \cdot \frac{{n - 4}}{n} = \frac{{8n - 32}}{{n^2 }}\\
\end{array}
$
Zelfde als hierboven maar nu zonder terugleggen geeft:
$
\begin{array}{l}
P(0\,\,rood) = \large\frac{{n - 4}}{n} \cdot \frac{{n - 5}}{{n - 1}} = \frac{{n^2 - 9n + 20}}{{n^2 - n}} \\
P(1\,\,rood) = 2 \cdot \large\frac{4}{n} \cdot \frac{{n - 4}}{{n - 1}} = \frac{{8n - 32}}{{n^2 - n}} \\
\end{array}
$
|
Klein steekproef uit grote populatie
Bij een kleine steekproef uit een grote populatie mag je trekken zonder terugleggen opvatten als trekken met terugleggen.
Je gaat er van uit dat de kans op 'succes' nauwelijk verandert als de steekproef relatief klein is ten opzichte van de populatie.
Voorbeeld
Je hebt een vaas met 100 rode en 300 witte knikker. Je pakt 3 knikkers uit de vaas. Noem het aantal rode knikkers $X$ en bereken de kans op minstens 1 rode knikker. Doe dit zowel met als zonder terugleggen.
|







