|
Recht evenredig
Als twee variabelen $x$ en $y$ (recht-)evenredig zijn dan wil dat zeggen dat als je de ene variabele met $k$ vermenigvuldigt dan moet je de andere variabele ook met $k$ vermenigvuldigen.
De verhouding $\frac{y}{x}$ is constant, dus $\frac{y}{x}=a$ ofwel $y=ax$.
De grafiek is een lijn door de oorsprong.
|
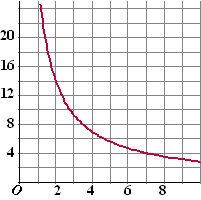
Omgekeerd evenredig
Als twee variabelen $x$ en $y$ omgekeerd evenredig zijn dan wil dat zeggen dat als je de ene variabele met $k$ vermenigvuldigt dan moet je de andere variabele met $\frac{1}{k}$ vermenigvuldigen.
Het product $xy$ is constant, dus $xy=a$ ofwel $y=\frac{a}{x}$.
De grafiek is een hyperbool.
|
|
Evenredig met een macht van x
$y$ is evenredig met $x^n$ betekent dat een getal $a$ bestaat zo, dat $y=ax^n$
|
Omgekeerd evenredig met een macht van x
$y$ is omgekeerd evenredig met $x^n$ betekent dat er een getal $a$ bestaat zo, dat $y=\frac{a}{x^n}$
|