|
Verzamelingen
Een getalverzameling is een verzameling van getallen met een bepaalde eigenschap.
De verzameling van de natuurlijke getallen:
$\mathbb{N}=\{ 0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,...\}$
De getallen 0, 1, 2, 3, ... zijn de elementen van de verzameling $\mathbb{N}$. Notatie: $0 \in\mathbb{N}$ of $-1\notin\mathbb{N}$
$\mathbb{N}$: natuurlijke getallen
$\mathbb{Z}$: gehele getallen
$\mathbb{Q}$: rationale getallen
$\mathbb{R}$: reële getallen
$\mathbb{C}$: complexe getallen
De verzameling die geen enkel element bevat heet de lege verzameling. Notatie: $\emptyset$
|
Vier manieren om een verzameling te noteren
-
De elementen van de verzameling opsommen tussen accolades.
$\left\{ {1,\,\,4,\,\,9,\,\,16} \right\}$
-
Met behulp van stippen een opsomming tussen accolades te suggereren.
$\left\{ {1,\,\,1,\,\,2,\,\,3,\,\,5,\,\,8,\,\,13,\,\,...} \right\}$
-
Het vermelden van een voorwaarde waaraan de elementen moeten voldoen.
$\left\{ {x \in\mathbb{N}|x^2 - 4x = 0} \right\}$
-
Met een interval.
$\left\{ {x \in\mathbb{R}|3 < x \le 11} \right\}$
|
|
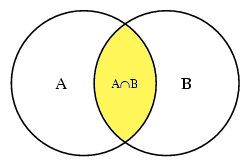
Vereniging
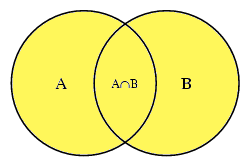
De vereniging $A \cup B$ bestaat uit de elementen die tot $A$, tot $B$ of tot beide behoren.
$
A \cup B = \left\{ {x|x \in A \vee x \in B} \right\}
$
|
Verschil
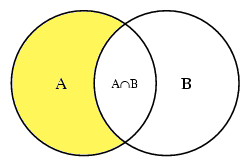
Het verschil $A\backslash B$ bestaat uit de elementen die wel tot $A$, maar niet tot $B$ behoren.
$
A\backslash B = \left\{ {x|x \in A \wedge x \notin B} \right\}
$
|