6. tellen met en zonder herhaling

Boomdiagram Je gooit 3 keer met een euro (kop of munt). Hoeveel verschillende uitkomsten zijn er als de volgorde van belang is? Zijn de mogelijke uitkomsten van a. allemaal even waarschijnlijk? Hoeveel uitkomsten zijn er als de volgorde niet van belang is? Zijn de mogelijk uitkomsten van c. allemaal even waarschijnlijk? Antwoorden Er zijn er 8. Als het een eerlijke munt is dan zijn de 8 mogelijkheden van a. even waarschijnlijk. Dat zijn er dan 4: 0, 1, 2 of 3 keer kop. Nee. De kans op (bijvoorbeeld) 2 kop is groter dan de kans op 3 kop. $P(2\,kop)=\frac{2}{8}$ $P(3\,kop)=\frac{1}{8}$

Wegendiagram Hoeveel 'codes' kan je maken met drie keer kiezen uit drie verschillende letters? Om van I. naar IV. te komen zijn er steeds 3 verschillende wegen. Het totaal aantal manieren om van I. naar IV. te gaan is 27. Er zijn 27 verschillende codes.

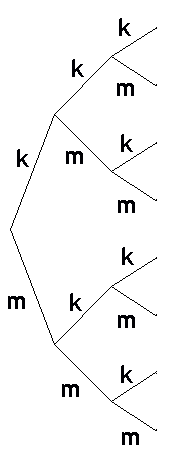
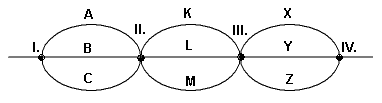
Vermenigvuldigingsregel Een gecombineerde handeling, die bestaat uithandeling I die op $p$ manieren kan worden uitgevoerd én handeling II die op $q$ manieren kan worden uitgevoerd én handeling III die op $r$ manieren kan worden uitgevoerd, kan op $p\times q\times r$ manieren worden uitgevoerd. Voorbeeld Je maakt getallen van 3 cijfers. Het eerste cijfer mag geen nul zijn en het laatste cijfer moet even zijn. Hoeveel getallen kan je maken? Uitwerken Voor het eerste cijfer kan je kiezen uit 9 cijfers $(p)$ Voor het tweede cijfer kan je kiezen uit 10 cijfers $(q)$ Voor het laatste cijfer kan je kiezen uit 5 $(r)$ Je kunt $p\times q\times r=9·10·5=450$ getallen maken.

Met en zonder herhaling Het is bij telproblemen belangrijk je af te vragen of herhalingen  zijn toegestaan. Voorbeelden Je verdeelt 3 keer 1000 euro over een groep van 50 mensen. Op hoeveel manieren kan dat? Uit een groep van 50 mensen moeten er 3 verplicht met prepensioen. Op hoeveel manieren kan je 3 mensen kiezen uit een groep van 50? Uit een groep van 50 mensen moet je een voorzitter, een penningmeester en een koffiejuffrouw (m/v) kiezen. Op hoeveel manieren kan dat? Uitwerking Is dit nu met of zonder herhaling? Dat is niet duidelijk. Met herhaling geeft $50·50·50=125.000$ manieren. Zonder herhaling is dat $50·49·48=117.600$ manieren. Dit is zonder herhaling. Je kunt niet iemand 3x met prepensioen sturen, denk ik... Het kan op $\eqalign{\frac{117.600}{6}=19.600}$ manieren. Dit is ook zonder herhaling. Nu is de volgorde wel van belang. Dit kan op $50·49·48=117.000$ manieren.

• een ander voorbeeld
• met of zonder herhaling

©2004-2024 W.v.Ravenstein