|
Hoeken berekenen
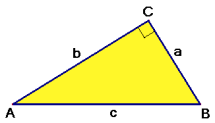
$
\eqalign{
& \sin \angle B = \frac{b}
{c} \cr
& \cos \angle B = \frac{a}
{c} \cr
& \tan \angle B = \frac{b}
{a} \cr}
$
Afspraak
Bij het berekenen van een hoek geef je het antwoord in één decimaal nauwkeurig, tenzij iets anders gevraagd wordt.
Gelijkvormigheid
Twee driehoeken zijn gelijkvormig als ze twee gelijke hoeken hebben.
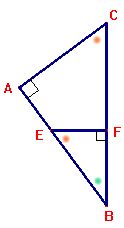
$
\Delta ABC \sim \Delta FBE
$
|
Lijnstukken berekenen
Bij het berekenen van lijstukken met behulp van de sinus, cosinus of tangens kun je gebruik maken van een verhoudingstabel.
Voorbeeld
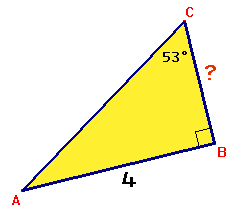
Aanpak
Kijkend vanuit $\angle C$ gaat het om $AB$ en $BC$. Dat zijn de overstaande en aanliggende rechthoekzijden dus ik ga iets doen met de tangens.
Uitwerking

$BC·tan(53^o)=4$
$\eqalign{BC=\frac{4}{tan(53^o)}\approx3,0}$
|
|
Gelijkvormigheid
|
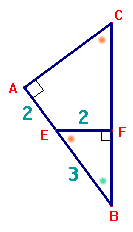
|
Opdracht 1
Gegeven: BE=3, AE=2 en EF=2
Gevraagd: bereken $\angle C$ in hele graden.
|
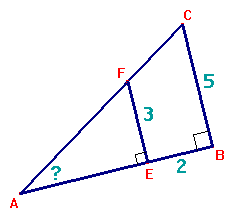 |
Opdracht 2
Gegeven: BC=5, EF=3 en EB=2.
Gevraagd: bereken $\angle A$ in hele graden.
|
|
Werkschema
Gebruik het volgende werkschema:
-
Verdiep je in de situatie
-
Maak een schets en zoek een rechthoekige driehoek. Teken zo nodig een hulplijn.
-
Los het probleem op met behulp van goniometrische verhoudingen. Denk ook aan de stelling van Pythagoras en gelijkvormigheid.
-
Beantwoord de vraag en controleer of het antwoord kan kloppen.
-
Vermeld, indien van toepassing, de eenheid.
|












